Có bao nhiêu nghiệm thực mà phương trình sau đây có? x6 - 3x4 + 3x2 - 1 = 0

Những câu hỏi liên quan
Phương trình sau đây có bao nhiêu nghiệm âm: x 6 + 2003 x 3 - 2005 = 0
A. 0
B. 1
C. 2
D. 6
Đặt t = x 3 thì phương trình x 6 + 2003 x 3 - 2005 = 0 trở thành
t 2 + 2003 t - 2005 = 0
Vì 1 . - 2005 < 0 suy ra phương trình ẩn t có 2 nghiệm trái dấu
Suy ra có phương trình đã cho có một nghiệm âm.
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Đồ thị (C) :
x
6
-
3
x
4
+
3
x
2
có bao nhiêu điểm cực trị ?
Đọc tiếp
Đồ thị (C) : x 6 - 3 x 4 + 3 x 2 có bao nhiêu điểm cực trị ?
![]()
![]()
![]()
![]()
Phương trình sau có bao nhiêu nghiệm: 1 + 3 x 2 = 2 x
A. 0 B. 1
C. 2 D. Vô số
Cho hàm số
f
x
x
3
-
3
x
2
+
2
có đồ thị là đường cong trong hình bên.Hỏi phương trình
x
3
-
3
x
2
+
2
3...
Đọc tiếp
Cho hàm số f x = x 3 - 3 x 2 + 2 có đồ thị là đường cong trong hình bên.
Hỏi phương trình
x 3 - 3 x 2 + 2 3 - 3 x 3 - 3 x 2 + 2 2 + 2 = 0 có bao nhiêu nghiệm thực phân biệt?

A. 7.
B. 9.
C. 6.
D. 5.
Phương trình x 3 - 3 x 2 - m 2 = 0 (với m là tham số thực) có nhiều nhất bao nhiêu nghiệm phân biệt
A. 4 nghiệm.
B. 3 nghiệm.
C. 2 nghiệm.
D. 6 nghiệm.
Đáp án B
Phương pháp:
Số nghiệm của phương trình |x3| - 3x2 - m2 = 0 bằng số giao điểm của đồ thị hàm số y = |x|3 - 3x2 và đường thẳng y = m2
Phác họa đồ thị hàm số , từ đó nhận xét số giao điểm trên.
Cách giải:
Số nghiệm của phương trình |x3| - 3x2 - m2 = 0 bằng số giao điểm của đồ thị hàm số y = |x|3 - 3x2 và đường thẳng y = m2
Từ đồ thị hàm số y = x3 - 3x2
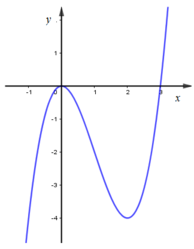
Ta vẽ được đồ thị hàm số y = |x|3 - 3x2 như sau:
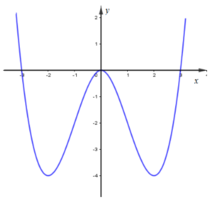
Do m2 ≥ 0,∀m nên đồ thị hàm số y = |x|3 - 3x2 cắt đường thẳng y = m2 tại nhiều nhất 3 điểm.
Đúng 0
Bình luận (0)
Cho hàm số
f
x
x
3
−
3
x
2
+
2
có đồ thị là đường cong trong hình bên. Hỏi phương trình
x
3
−
3
x
2
+
2
3...
Đọc tiếp
Cho hàm số
f
x
=
x
3
−
3
x
2
+
2
có đồ thị là đường cong trong hình bên. Hỏi phương trình
x
3
−
3
x
2
+
2
3
−
3
x
3
−
3
x
2
+
2
2
+
2
=
0
có bao nhiêu nghiệm thực dương phân biệt? 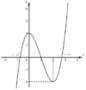
A. 3
B. 5
C. 7
D. 1
Đáp án C

Chú ý và sai lầm: Sau khi đặt ẩn phụ và tìm ra được 3 nghiệm t, nhiều học sinh kết luận sai lầm phương trình có 3 nghiệm phân biệt và chọn đáp án A. Số nghiệm của phương trình là số nghiệm x chứ không phải số nghiệm t.
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của m để phương trình sau vô nghiệm
x
6
+
3
x
5
+
6
x
4
−
m
x
3
+
6
x
2
+
3
x
+
1
0
A. Vô số B. 26 C. 27 D. 28
Đọc tiếp
Có bao nhiêu giá trị nguyên của m để phương trình sau vô nghiệm x 6 + 3 x 5 + 6 x 4 − m x 3 + 6 x 2 + 3 x + 1 = 0
A. Vô số
B. 26
C. 27
D. 28
Có bao nhiêu giá trị nguyên của m để phương trình sau vô nghiệm:
x 6 + 3 x 5 + 6 x 4 - m x 3 + 6 x 2 + 3 x + 1 = 0
A. Vô số
B. 26
C. 27
D. 28
Đáp án C.
⇒ Chia 2 vế phương trình cho x 3 ta được:
x 3 + 1 x 3 + 3 x 2 + 1 x 2 + 6 x + 1 x = m (*)
Đặt t = x + 1 x ⇒ t ≥ 2 , phương trình (*) m = t 3 + 3 t 2 + t - 6
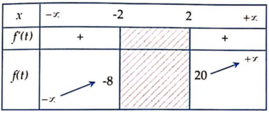
Xét f ( t ) = t 3 + 3 t 2 + 3 t - 6 trên ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
f ' ( t ) = 0 ⇔ t = - 1
Bảng biến thiên:
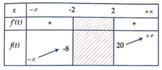
⇒ f ( t ) ∈ ( - ∞ ; - 8 ] ∪ [ 20 ; + ∞ ) ∀ t ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
⇒ Phương trình f (t) vô nghiệm ⇔ m ∈ - 8 ; 20
⇒ Có 27 giá trị m nguyên thỏa mãn.
Đúng 0
Bình luận (0)
Không phải lớp 3 nhe nhầm lớp rùi
Có bao nhiêu số nguyên m để bất phương trình
x
6
+
6
x
4
+
15
-
3
m
2
x
2
-...
Đọc tiếp
Có bao nhiêu số nguyên m để bất phương trình x 6 + 6 x 4 + 15 - 3 m 2 x 2 - 6 m x + 10 ≥ 0 nghiệm đúng với mọi số thực x.
A. 4
B. 3
C. Vô số
D. 5
Chọn đáp án D.
Bất phương trình tương đương với
![]()
![]()
![]()
![]()
![]()
trong đó hàm số f t = t 3 + 3 t đồng biến trên R
Vậy y c b t ⇔ x 2 - m x + 1 ≥ 0 , ∀ x
![]()
Có 5 số nguyên thoả mãn
Đúng 0
Bình luận (0)