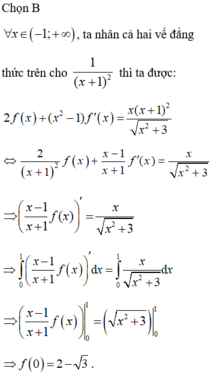Số trong đẳng thức trên có giá trị là

Những câu hỏi liên quan
*3+1/2*3*4+1/3*4*5+...+1/98*99*100 = 1/k * (1/1*2-1/99*100)
Số k trong đẳng thức trên có giá trị là
nhớ giúp mình nha
\(\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...\frac{1}{98.99.100}=\frac{1}{k}.\left(\frac{1}{1.2}-\frac{1}{99.100}\right)\)
Số trong đẳng thức trên có giá trị là
\(\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+....+\frac{1}{98.99.100}=\frac{1}{k}\left(\frac{1}{1.2}-\frac{1}{99.100}\right)\)
\(\Leftrightarrow\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+...+\frac{1}{98.99}-\frac{1}{99.100}\right)=\frac{1}{k}\left(\frac{1}{1.2}-\frac{1}{99.100}\right)\)
\(\Leftrightarrow\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{99.100}\right)=\frac{1}{k}\left(\frac{1}{1.2}-\frac{1}{99.100}\right)\)
\(\Leftrightarrow\frac{1}{k}=\frac{1}{2}\Rightarrow k=2\)
Đúng 0
Bình luận (0)
\(\frac{1}{1.2.3}+\frac{1}{2.3.4}+....+\frac{1}{98.99.100}=\frac{1}{k}.\left(\frac{1}{1.2}-\frac{1}{99.100}\right)\)
Số K trong đẳng thức trên có giá trị là..
\(\frac{1}{1.2.3}+\frac{1}{2.3.4}+.......+\frac{1}{98.99.100}=\frac{1}{k}\left(\frac{1}{1.2}-\frac{1}{99.100}\right)\)
\(\Leftrightarrow\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+....+\frac{1}{98.99}-\frac{1}{99.100}\right)=\frac{1}{k}\left(\frac{1}{1.2}-\frac{1}{99.100}\right)\)
\(\Leftrightarrow\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{99.100}\right)=\frac{1}{k}\left(\frac{1}{1.2}-\frac{1}{99.100}\right)\)
\(\Leftrightarrow\frac{1}{2}=\frac{1}{k}\)
\(\Rightarrow k=2\)
Đúng 0
Bình luận (0)
\(\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+.............+\frac{1}{98.99.100}=\frac{1}{k}.\left(\frac{1}{1.2}-\frac{1}{99.100}\right)\). Số k trong đẳng thức trên có giá trị là
\(\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...+\frac{1}{98.99.100}=\frac{1}{k}.\left(\frac{1}{1.2}-\frac{1}{99.100}\right)\).Số k trong đẳng thức trên có giá trị là ......
Bày cách làm giùm mình nha !
Những số nào trong các số -4,-3,-2,-1,0,1,2,3,4 là giá trị của số nguyên x thoả mãn đẳng thức: x.(4 + x) = -3
Ta có: -3 = 3.(-1) = 1.(-3)
Như vậy các số thoả mãn đẳng thức trên chỉ có thể là -3; 1; 3 hoặc -1
Do x < 4 + x nên x chỉ có thể bằng -1 hoặc – 3.
Với x = -3 ta có: 4 + x = 4 + (-3) =1 => (-3).1 = -3 (thoả mãn)
Với x = -1 ta có: 4 + x = 4 + (-1) = 3 => (-1).3 = -3 (thoả mãn)
Vậy x = -3 hoặc x = -1
Đúng 0
Bình luận (0)
Cho hàm số f(x) có đạo hàm trên
-
1
;
+
∞
.Biết đẳng thức
2
f
x
+
x
2
-
1
f
x...
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên - 1 ; + ∞ .Biết đẳng thức 2 f x + x 2 - 1 f ' x = x x + 1 2 x 2 + 3 được thỏa mãn ∀ x ∈ - 1 ; + ∞ . Tính giá trị f(0).
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D.Chưa đủ dữ kiện tính ![]() .
.
\(\frac{1}{1\cdot2\cdot3}+\frac{1}{2\cdot3\cdot4}+\frac{1}{3\cdot4\cdot5}+.....+\frac{1}{98\cdot99\cdot100}=\frac{1}{k}\cdot\left(\frac{1}{1\cdot2}-\frac{1}{99\cdot100}\right)\)
Số k trong đẳng thức trên có giá trị là ?
\(\frac{2}{n\left(n+1\right)\left(n+2\right)}=\frac{n+2-n}{n\left(n+1\right)\left(n+2\right)}=\frac{n+2}{n\left(n+1\right)\left(n+2\right)}-\frac{n}{n\left(n+1\right)\left(n+2\right)}=\frac{1}{n\left(n+1\right)}-\frac{1}{n\left(n+2\right)}\)
\(\Rightarrow\frac{2}{1.2.3}+\frac{2}{2.3.4}+...+\frac{2}{98.99.100}=\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+...+\frac{1}{98.99}-\frac{1}{99.100}\)
\(=\frac{1}{1.2}-\frac{1}{99.100}\)
\(\Rightarrow\frac{1}{1.2.3}+...+\frac{1}{98.99.100}=\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{99.100}\right)\)
\(\Rightarrow k=2\)
Đúng 0
Bình luận (0)