\(ƯCLN\left(x;y\right)=\frac{xy}{BCNN\left(x;y\right)}=\frac{20}{10}=2\)

Đặt \(x=2k,y=2t\) (y và t là 2 số nguyên tố cùng nhau)

\(xy=20\Rightarrow2k.2t=20\Rightarrow k.t=5\)

\(\Rightarrow k\inƯ\left(5\right)=\left\{1;5\right\}\)

\(\Rightarrow x=2k\in\left\{2;10\right\}\)

Nếu x = 2 thì y = 10

Nếu x = 10 thì y = 2

Vậy x = 2 và y = 10 hoặc x = 10 và y = 2

Khó zậy

cho anh 1 tích đứng

aefklhhgrs

ánkjnƯHRBVW

asbfsj,hbgbqae

aerkljhtgr

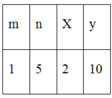
- Đặt (x; y) = d  nên x = d.m; y = d.n với (m;n) =1. Giả sử x ≤ y thì  m ≤ n.

- Ta có: x.y = dm.dn= d².mn

BCNN(x; y) =  x y x ; y = d 2 m . n d = d . m . n

- Ta có: BCNN (x;y) = 10 và x. y = 20 nên d = x y B C N N ( x ; y ) = 20 10 = 2

=> 2.m.n =10 nên m.n = 5

Bảng giá trị

đã đúng

bài 1 : 

a) x - {x-[(-x-1)]} = 1

=> x -{x -[2x-1]} =1

=> x - {x-2x+1} =1

=> x - ( -1+1)=1

=> x+x-1 = 1

=> 2x = 2

=> x =1

vậy x = 1

b) ( x+5).(x-2)<0

=> x+5 và x-2 là 2 thừa số trái dấu

mà x-2 < x+5

=> x-2 âm => x<2

   x+5 dương=> x > -5

=> -5 < x<2

vậy ....

Bài 2 :

( x+1).(xy-1) = 3

vì x,y thuộc Z => x+1 thuộc Z , xy-1 thuộc Z

=> x + 1 avf xy -1 là các ước nguyên của 3

từ đó tìm được các giá trị

 + nếu x = -2 => y=1

+ nếu x = 2 => y =1

+ nếu x = -4 => y =0

b) 3x+4y-xy =15

x.(3-y)+4y = 15 x.(3-y)=15-4y

x.(3-y)=12-4y+3

x.(3-y) = 4.(3-y)+3

x.(3-y)-4.(3-y)=3

vì x,y thuộc Z => 3-y thuộc Z , x-4 thuộc Z

=> 3-y và x-4  là các ước nguyễn của 3

=>..... 

ta tìm được các giá trị của x và y

Bài 3:

nếu x = 0  thì 26^x = 1 khác 25^y + 24^z với mọi y, z thuộc N, loại

=> x lớn hơn hoặc = 1

=> 26^x chẵn

mà 25^y lẻ  với mọi y thuộc N

=> 24^7 lẻ => z =0

ta có 26^x = 25^y + 1 

với x = y+ 1 thì 26 = 25 +1 , đúng

với x > 1, y > 1 thì 26^x có 2 c/s t/c là 76

=> 26^x chia hết cho 4

25^y có 2 c/s t/c là 25 => 25^y chia 4 dư 1

=> 25 ^y + 1 chia 4 dư 2

=> 26^x khác 25^y + 1 , loại

Bài 4:

ta công tất cả các ( x-y)+(y-x)+(z+x) = 2012

đó là 2 lần x => x= 1006

rùi thay

ta có đ/s :

 z =1007

y = -1005

Bài 5 :

do 20/39 là phân số tối giản

có UWCLN ( 20,39 ) =1

mà phân số cần tìm UWCLN của tử và mẫu là 36

=> phân số cần tìm là :

20.36/39.36

= 720.1404

Đ/S: 720/1404

Bài 6 :

vì UWClN ( a,b) = 12 => a =12 m, b =12n

( m,n ) =1

BCNN ( a,b )  =12 .m.n =180

=> m.n = 15

do vai trò a,b bình đẳng, giải sử a lớn hơn hoặc bằng b

=> m lớn hơn hoặc bằng n

mà ( m,n ) =1 => m =15, n= 1

hoặc m =5, n =3

vậy vs a =180=> b=12

vs a = 60 => b =36

Bài 7 :

gọi UWCLN ( a,b ) = d ( d thuộc N*)

=> a = d .m, b = d . n

( m,n)=1

BCNN ( a,b) = d . m. n

mà UWCLN (a,b )+ BCNN (a,b ) = 23

=> d + dmn = 23

=> d .( 1+mn) =23

........  v.v

tử từng t/h

Đ/S : vs m = 2 2 => n=1 hoặc m=11, n=2

vs a = 22 => b =1 hoặc a =11 => b = 2

Bài 7:Đ/s : x=1,y=1

x=3, y=2

x=1,y=2

x=2,y=3

x=2,y=1

BCNN (x,y) x UCLN ( x,y ) = a . b

Gọi UCLN ( x, y ) = d => x chia hết cho d => x = d.a

                                       y chia hết cho d => y = d.b

Trong đó, UCLN (a,b) = 1

 Từ đề bài, BCNN(x,y) = 6 . d

 => BCNN ( x,y ) . UCLN ( x,y ) = 6.d.d

( Nhân 2 vế với UCLN (x,y) = d

 => x . y = 6 . d^2

    d.a . d.b = 6 . d^2

      d^2. a.b= 6.d^2

=>         a.b = 6

 Sau đó ta lập bảng, dùng phương pháp loại trừ tìm a,b và tìm được  2 trường hợp x,y :

 x = 12 ; y = 18

x = 18 ; y = 12

biết a và b là 2 số tự nhiên không chia hết cho 2 . hoi tổng a+b chia hết cho 2 không