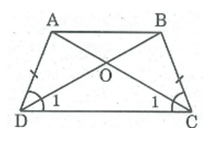
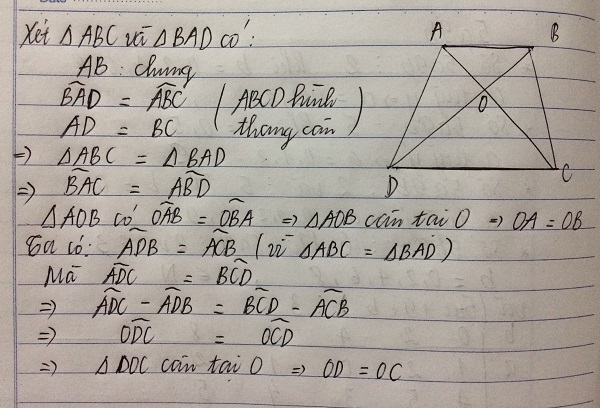Hình thang cân ABCD có AB//CD.Gọi O là giao điểm của 2 đường chéo. CMR: OA=OB, OC=OD

Những câu hỏi liên quan
Cho hình thang cân ABCD có AB//CD, o là giao điểm của hai đường chéo, e là đường thẳng chứa cạnh bên AD và BC. CMR:
a, OA=OB, OC=OD
b, CM: EO là đường trung trực của 2 đáy hình thang ABCD
a: Xét ΔADC và ΔBCD có
AD=BC
\(\hat{ADC}=\hat{BCD}\) (ABCD là hình thang cân)
DC chung
Do đó: ΔADC=ΔBCD
=>\(\hat{ACD}=\hat{BDC}\)
=>\(\hat{OCD}=\hat{ODC}\)
=>OC=OD
ta có: OC+OA=AC
OD+OB=BD
mà OC=OA và AC=BD
nên OA=OB
b: Xét ΔECD có \(\hat{ECD}=\hat{EDC}\)
nên ΔECD cân tại E
=>EC=ED
=>E nằm trên đường trung trực của CD(3)
Ta có: OC=OD
=>O nằm trên đường trung trực của CD(4)
Từ (3),(4) suy ra EO là đường trung trực của CD
Ta có: EA+AD=ED
EB+BC=EC
mà AD=BC và ED=EC
nên EA=EB
=>E nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra EO là đường trung trực của AB
Đúng 0
Bình luận (0)
Hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo. Chứng minh rằng OA = OB, OC = OD.
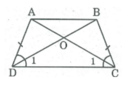
Xét ∆ ADC và ∆ BCD, ta có:
AD = BC (tính chất hình thang cân)
∠ (ADC) = ∠ (BCD) (gt)
DC chung
Do đó: ∆ ADC = ∆ BCD (c.g.c) ⇒ ∠ C 1 = ∠ D 1
Trong ∆ OCD ta có: ∠ C 1 = ∠ D 1 ⇒ ∆ OCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.
Đúng 3
Bình luận (0)
hình thang cân ABCD có AB // CD , O là giao điểm của hai đường chéo. Chứng minh rằng OA =OB , OC = OD
Hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo. Chứng minh rằng OA = OB, OC = OD ?
hình thang cân ABCD có AB//CD , O là giao điểm của hai đường chéo .Chứng minh rằng OA=OB, OC=OD
Xét tam giác OAD và tam giác OBC ta có:
góc OAD = góc OCB (hai góc so le trong, AB//CD)
AD = BC (Vì hình thang cân có hai cạnh bên bằng nhau)
góc ODA = góc OBC (hai góc so le trong, AB//CD)
=> tam giác OAD = tam giac OBC (g-c-g)
=> OA=OB
chứng minh tương tự ta sẽ được OD=OC
Đúng 0
Bình luận (0)
Bài làm :
Xét tam giác ABC và tam gác BAD có :
AB cạnh chung
BC = AC ( ABCD httg cân )
AC = BD ( 1 ) ( ABCD httg cân )
\(\Rightarrow\)tam giác ABC = tam giác BAD ( c - c - c )
\(\Rightarrow\widehat{A1}\)= \(\widehat{D1}\)
\(\Rightarrow\)Tam giác OAB cân tại O
\(\Rightarrow\)OA = OB ( 2 )
ta có : OA + OC = AC ( 3 )
OB + OD = BD ( 4 )
Từ ( 1 ) : ( 2 ) ; ( 3 ) ; ( 4 ) suy ra OC = OD
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình thang cân ABCD có AD // BC, AB = DC. gọi O là giao điểm 2 đường chéo AC và BD . C/m OA = OC OB = OD
Bài 1: cho hình thang cân ABCD có AB<CD,o là giao điểm của hai đường chéo,E là giao điểm của hai đường thẳng chứa cạnh bên AD và BC.Cm
a,OA=OB,OC=OD
b,EO là đường trung trực của hai đáy hình thang ABCD
a ) Xét ADC và BCD, ta có:
AD = BC (tính chất hình thang cân)
(ADC) = (BCD) (gt)
DC chung
Do đó: ADC = BCD (c.g.c) ⇒ =
Trong OCD ta có: = ⇒ OCD cân tại O ⇒ OC = OD (1)
AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO.
b)
⇒ ∆ OCD cân tại O
⇒ OC = OD
⇒ OA + AD = OB + BC
Mà AD = BC (tính chất hình thang cân)
⇒ OA = OB
Xét ∆ ADC và ∆ BCD :
AD = BC (chứng minh trên)
AC = BD (tính chất hình thang cân)
CD cạnh chung
Do đó: ∆ ADC = ∆ BCD (c.c.c)
⇒ ∆ EDC cân tại E
⇒ EC = ED nên E thuộc đường trung trực của CD
OC = OD nên O thuộc đường trung trực của CD
E≢ O. Vậy OE là đường trung trực của CD.
BD = AC (chứng minh trên)
⇒ EB + ED = EA + EC mà ED = EC
⇒ EB = EA nên E thuộc đường trung trực AB
E≢ O. Vậy OE là đường trung trực của AB.
Đúng 0
Bình luận (0)
Bài 1: Cho hình thang cân ABCD có AB//CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa cạnh bên AD và BC. Chứng minh:
a) OAOB , OCOD
b) EO là đường trung trực của hai đáy hình thang ABCD.
Bài 2: Cho hình thang ABCD (AD//BC, ADBC) có đường chéo AC vuông góc với cạnh bên CD, AC là tia phân giác góc BAD và góc D60 độ
a) Chứng minh ABCD là hình thang cân
b) Tính độ dài cạnh AD, biết chu vi hình th...
Đọc tiếp
Bài 1: Cho hình thang cân ABCD có AB//CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa cạnh bên AD và BC. Chứng minh:
a) OA=OB , OC=OD
b) EO là đường trung trực của hai đáy hình thang ABCD.
Bài 2: Cho hình thang ABCD (AD//BC, AD>BC) có đường chéo AC vuông góc với cạnh bên CD, AC là tia phân giác góc BAD và góc D=60 độ
a) Chứng minh ABCD là hình thang cân
b) Tính độ dài cạnh AD, biết chu vi hình thang bằng 20cm.
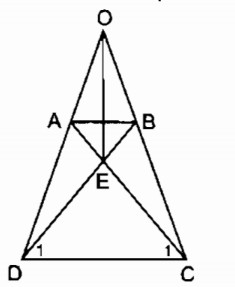
Bài 3: Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD=AE
a) Tứ giác BDEC là hình gì ? Vì sao?
b) Các điểm D,E ở vị trí nào thì BD=DE=EC?
Mình đang cần gấp. Giúp mình nhé cảm ơn các bạn
Bài 3:
a: Xét ΔABC có \(\frac{AD}{AB}=\frac{AE}{AC}\)
nên DE//BC
Xét tứ giác BDEC có DE//BC và \(\hat{DBC}=\hat{ECB}\) (ΔABC cân tại A)
nên BDEC là hình thang cân
b: BDEC là hình thang cân
=>BD=EC
DB=DE
=>ΔDBE cân tại D
=>\(\hat{DEB}=\hat{DBE}\)
mà \(\hat{DEB}=\hat{EBC}\) (hai góc so le trong, DE//BC)
nên \(\hat{DBE}=\hat{CBE}\)
=>BE là phân giác của góc ABC
=>E là chân đường phân giác kẻ từ B xuống AC
ED=EC
=>ΔEDC cân tại E
=>\(\hat{EDC}=\hat{ECD}\)
mà \(\hat{EDC}=\hat{BCD}\) (hai góc so le trong, DE//BC)
nên \(\hat{ECD}=\hat{BCD}\)
=>\(\hat{ACD}=\hat{BCD}\)
=>CD là phân giác của góc ACB
=>D là chân đường phân giác kẻ từ C xuống AB
Bài 2:
a: ΔCAD vuông tại C
=>\(\hat{CAD}+\hat{CDA}=90^0\)
=>\(\hat{CAD}=90^0-60^0=30^0\)
AC là phân giác của góc BAD
=>\(\hat{BAD}=2\cdot\hat{CAD}=60^0\)
Xét hình thang ABCD có \(\hat{BAD}=\hat{CDA}\left(=60^0\right)\)
nên ABCD là hình thang cân
b: BC//AD
=>\(\hat{BCA}=\hat{CAD}\) (hai góc so le trong)
mà \(\hat{CAD}=\hat{BAC}\) (AC là phân giác của góc BAD)
nên \(\hat{BCA}=\hat{BAC}\)
=>BC=BA
=>BC=BA=CD
Xét ΔCAD vuông tại C có cos CDA=\(\frac{CD}{DA}\)
=>\(\frac{CD}{DA}=cos60=\frac12\)
=>CD=0,5AD
=>BC=BA=CD=0,5AD
Chu vi hình thang ABCD là 20cm
=>AB+BC+CD+DA=20
=>0,5AD+0,5AD+0,5AD+AD=20
=>2,5AD=20
=>AD=8(cm)
Bài 1:
a: Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
Do đó: ΔADC=ΔBCD
=>\(\hat{ACD}=\hat{BDC}\)
=>\(\hat{ODC}=\hat{OCD}\)
=>OD=OC
Ta có: OD+OB=BD
OC+OA=AC
mà BD=AC và OD=OC
nên OB=OA
b: Xét ΔEDC có AB//DC
nên \(\frac{EA}{AD}=\frac{EB}{BC}\)
mà AD=BC
nên EA=EB
=>E nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra EO là đường trung trực của AB
Ta có: EA+AD=ED
EB+BC=EC
mà EA=EB và AD=BC
nên ED=EC
=>E nằm trên đường trung trực của DC(3)
Ta có: OC=OD
=>O nằm trên đường trung trực của CD(4)
Từ (3),(4) suy ra EO là đường trung trực của CD
Đúng 0
Bình luận (0)
Bài 1: Cho hình thang cân ABCD có AB//CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa cạnh bên AD và BC. Chứng minh:
a) OAOB , OCOD
b) EO là đường trung trực của hai đáy hình thang ABCD.
Bài 2: Cho hình thang ABCD (AD//BC, ADBC) có đường chéo AC vuông góc với cạnh bên CD, AC là tia phân giác góc BAD và góc D60 độ
a) Chứng minh ABCD là hình thang cân
b) Tính độ dài cạnh AD, biết chu vi hình th...
Đọc tiếp
Bài 1: Cho hình thang cân ABCD có AB//CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa cạnh bên AD và BC. Chứng minh:
a) OA=OB , OC=OD
b) EO là đường trung trực của hai đáy hình thang ABCD.
Bài 2: Cho hình thang ABCD (AD//BC, AD>BC) có đường chéo AC vuông góc với cạnh bên CD, AC là tia phân giác góc BAD và góc D=60 độ
a) Chứng minh ABCD là hình thang cân
b) Tính độ dài cạnh AD, biết chu vi hình thang bằng 20cm.
Bài 3: Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD=AE
a) Tứ giác BDEC là hình gì ? Vì sao?
b) Các điểm D,E ở vị trí nào thì BD=DE=EC?
Mình đang cần gấp. Giúp mình nhé cảm ơn các bạn
Bài 3:
a: Xét ΔABC có \(\frac{AD}{AB}=\frac{AE}{AC}\)
nên DE//BC
Xét tứ giác BDEC có DE//BC và \(\hat{DBC}=\hat{ECB}\) (ΔABC cân tại A)
nên BDEC là hình thang cân
b: BDEC là hình thang cân
=>BD=EC
DB=DE
=>ΔDBE cân tại D
=>\(\hat{DEB}=\hat{DBE}\)
mà \(\hat{DEB}=\hat{EBC}\) (hai góc so le trong, DE//BC)
nên \(\hat{DBE}=\hat{CBE}\)
=>BE là phân giác của góc ABC
=>E là chân đường phân giác kẻ từ B xuống AC
ED=EC
=>ΔEDC cân tại E
=>\(\hat{EDC}=\hat{ECD}\)
mà \(\hat{EDC}=\hat{BCD}\) (hai góc so le trong, DE//BC)
nên \(\hat{ECD}=\hat{BCD}\)
=>\(\hat{ACD}=\hat{BCD}\)
=>CD là phân giác của góc ACB
=>D là chân đường phân giác kẻ từ C xuống AB
Bài 2:
a: ΔCAD vuông tại C
=>\(\hat{CAD}+\hat{CDA}=90^0\)
=>\(\hat{CAD}=90^0-60^0=30^0\)
AC là phân giác của góc BAD
=>\(\hat{BAD}=2\cdot\hat{CAD}=60^0\)
Xét hình thang ABCD có \(\hat{BAD}=\hat{CDA}\left(=60^0\right)\)
nên ABCD là hình thang cân
b: BC//AD
=>\(\hat{BCA}=\hat{CAD}\) (hai góc so le trong)
mà \(\hat{CAD}=\hat{BAC}\) (AC là phân giác của góc BAD)
nên \(\hat{BCA}=\hat{BAC}\)
=>BC=BA
=>BC=BA=CD
Xét ΔCAD vuông tại C có cos CDA=\(\frac{CD}{DA}\)
=>\(\frac{CD}{DA}=cos60=\frac12\)
=>CD=0,5AD
=>BC=BA=CD=0,5AD
Chu vi hình thang ABCD là 20cm
=>AB+BC+CD+DA=20
=>0,5AD+0,5AD+0,5AD+AD=20
=>2,5AD=20
=>AD=8(cm)
Bài 1:
a: Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
Do đó: ΔADC=ΔBCD
=>\(\hat{ACD}=\hat{BDC}\)
=>\(\hat{ODC}=\hat{OCD}\)
=>OD=OC
Ta có: OD+OB=BD
OC+OA=AC
mà BD=AC và OD=OC
nên OB=OA
b: Xét ΔEDC có AB//DC
nên \(\frac{EA}{AD}=\frac{EB}{BC}\)
mà AD=BC
nên EA=EB
=>E nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra EO là đường trung trực của AB
Ta có: EA+AD=ED
EB+BC=EC
mà EA=EB và AD=BC
nên ED=EC
=>E nằm trên đường trung trực của DC(3)
Ta có: OC=OD
=>O nằm trên đường trung trực của CD(4)
Từ (3),(4) suy ra EO là đường trung trực của CD
Đúng 0
Bình luận (0)