5) Từ M thuộc BC của triangle ABC cân tại A kẻ song song AC cắt AB tại D Từ M kẻ Song song AB cắt AC tại E . Trên tia đối FM lấy EF = MD Chứng minh: a) AC = MD + ME b)ABMF hình bình hành

Những câu hỏi liên quan
Cho tam giác ABC cân tại A. M là trung điểm của AB . Từ M kẻ ME song song với BC,cắt AC tại E
a) Chứng minh tứ giác BMEC là hình thang cân
b) từ M kẻ MF song song với AC cắt BC tại F. Chứng minh tứ giác MECF là hình bình hành.
c) gọi I là trung điểm của MF. Chứng minh B,I,E thẳng hàng.
d) MC cắt EF tại K kẻ KH vuông góc với ME(H thuộc ME). Chứng minh FK^2=KH^2+1/4 IK^2.
Cho tam giác ABC cân tại A. Tia phân giác góc BAC cắt cạnh BC tại Ma) Chứng minh
∆
A
M
B
∆
A
M
C
.
b) Kẻ
M
E
⊥
A
B
(
E
∈
A
B
)
,
M
F
⊥
A
C
(
F
∈
A
C
)
. Chứng minh tam giác AEF cân.c) Chứng minh
A
M
⊥
E
F
....
Đọc tiếp
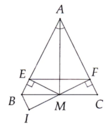
Cho tam giác ABC cân tại A. Tia phân giác góc BAC cắt cạnh BC tại M
a) Chứng minh ∆ A M B = ∆ A M C .
b) Kẻ M E ⊥ A B ( E ∈ A B ) , M F ⊥ A C ( F ∈ A C ) . Chứng minh tam giác AEF cân.
c) Chứng minh A M ⊥ E F .
d) Qua B kẻ đường thẳng song song với AC cắt đường thẳng FM tại I Chứng minh BE = BI
Cho tam giác ABC lấy M bất kì trên cạnh BC. Từ M kẻ đường song song với AB cắt AC tại D. Từ M kẻ đường thẳng song song với AC cắt AB tại E. Cm: ME=AD và MD=AE
Xét tứ giác AEMD có : MD // AE (vì MD // AB) và ME // AD (vì ME // AC)
=> AEMD là hình bình hành. Theo tính chất của hình bình hánh ta suy ra được ME = AD và MD = AE (đpcm).
Đúng 0
Bình luận (0)
Cho góc xoy=90°, điểm M nằm trong góc đó . Vẽ điểm A và B sao cho Ox là đường trung trực của MA, Oy là đường trung trực của MB . CM OA=OB
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác ABC cân tại A ( AB=AC>BC). trên cạnh BC lấy M sao cho MB < MC. Từ M kẻ dường thẳng song song với AC cắt AB tại E,kẻ đường thẳng song song với AB cắt AC tại F. gọi N là điểm đối xứng của M qua EF.
a) CHo AB= 1002,5 cm.TÍnh chu vi tứ giác AEMF
b) chứng minh tứ giác ANEF là hình thang cân
c)AN cắt BC tại H.chứng minh HB.HC= HN.HA
Cho tam giac abc có ab=3cm;ac=4cm;bc=5cm
a)tam giác abc là tam giác gì ?Tại sao?
b)gọi m là trung điểm của ab trên tia đối của mc lấy D sao cho md=mc.Chứng minh tam giác amc=tam giác bmd và bd song song ac
c)Kẻ trung tuyến be của tam giac abc (e thuộc ac) cắt mc tại g; qua e kẻ ef song song vói ab (f thuộc bc) . Chứng minh ba điểm a g f thẳng hàng
d) chứng minh be^2+cm^2=5/4bc^2
Cho tam giác ABC cân tại A, M là trung điểm của BC. Kẻ tia Mx song song với AC cắt AB tại E, kẻ tia Myvsong song với AB cắt AC tại F. Chứng minh EF là đường trung bình của tam giác ABC
Bạn tự vẽ hình
Tam giác ABC có:
M là trung điểm của BC và ME // AC
=> ME là đường trung bình của t/g ABC => BE=EA (1)
cm tương tự, ta có: MF là đường trung bình của t.g ABC và EF=FC (2)
Từ (1),(2) => EF là đường trung bình của t/g ABC
Vậy EF là đường trung bình của t/g ABC
Đúng 0
Bình luận (0)
Cho ∆ABC cân tại A ( góc A nhọn , AB>BC ) . Gọi M là trung điểm của BC. a) Chứng minh: ∆ABM=∆AMC. b) Kẻ MD vuông góc với AB tại D , kẻ ME vuông góc với AC tại E . Chứng minh : ∆EDM là tam giác cân. c) Qua M kẻ đường thẳng song song với AB , cắt cạnh AC tại F . Chứng minh : F là trung điểm của AC Giải giúp mình ạ
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
b: Xét ΔADM vuông tại D và ΔAEM vuông tại E có
AM chung
góc DAM=góc EAM
=>ΔADM=ΔAEM
=>MD=ME
=>ΔMED cân tại M
c: Xét ΔCAB có
M là trung điểm của CB
MF//AB
=>F là trung điểm của AC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A , lấy điểm D bất kỳ trên AB ,lấy điểm E trên tia đối của tia CA sao cho CE bằng BD từ D kẻ đường thẳng A song song với AC cắt BC tại F a.chứng minh MN=PQ b,MNPQ là hình bình hành
Cho tam giác ABC cân tại A, M là trung điểm của cạnh BC. Kẻ tia Mx song song
với AC cắt AB tại E, kẻ tia My song song với AB cắt AC tại F. Chứng minh:
a) EF là đường trung bình của tam giác ABC.
b) AM là đường trung trực của EF.
Mình không biết vẽ hình trên đây bạn tự vẽ hình nhé
Xét tam giác BAC có: BM=CM(M là trung điểm của BC)
ME//AC(Mx//AC)
=>AE=BE(hay E là trung điểm của AB)
Xét tam giác CBA có: BM=CM(M là trung điểm của BC)
MF//AB(My//AB)
=>AF=CF(hay F là trung điểm của AC)
Xét tam giác ABC có: AE=BE
AF=CF
=>EF là đường trung bình của tam giác ABC
b, Xét tứ giác AEMF có: ME//AF(Mx//AC)
MF//AE(My//AB)
=>AEMF là hình bình hành
Ta có: AE=BE; AF=CF
mà AB=AC(tam giác ABC cân tại A)
=>AE=BE=AF=CF
Xét hình bình hành AEMF có:AF=AE
=>AEMF là hình thoi
=> AM vuông góc với EF và AM đi qua trung điểm của EF
=>AM là đường trung trực của EF