điều kiện để 2 tam giác có cùng trọng tâm

Những câu hỏi liên quan
Cho tam giác ABC có AD là trung tuyến, G là trọng tâm của tam giác ABC. Trên tia đối của tia DC lấy M sao cho DM=DG.
a) Chứng minh rằng: tứ giác BGCM là Hình bình hành
b) Tam giác ABC thỏa mãn điều kiện gì để tứ giác BGCM là hình thoi
c) Thêm điều kiện của tam giác ABC cân để CM = AM/2
Điều kiện nào sau đây không là điều kiện cần và đủ để G là trọng tâm của tam giác ABC, với M là trung điểm của BC? A.
A
M
→
-
3
2
G
A
→
B.
2
G
M
→
G...
Đọc tiếp
Điều kiện nào sau đây không là điều kiện cần và đủ để G là trọng tâm của tam giác ABC, với M là trung điểm của BC?
A. A M → = - 3 2 G A →
B. 2 G M → = G A →
C. A G → + B G → + C G → = 0 →
D. G A → + G B → + G C → = 0 →
G là trọng tâm tam giác ABC khi và chỉ khi ít nhất 1 trong các điều kiện sau được thỏa mãn:
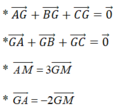
Đáp án B
Đúng 0
Bình luận (0)
G,G, lần lược là trọng tatam giác ABC và A,B,C, .C/m điều kiện cần và đủ để 2 tam gics có cùng trọng tâm là \(3\overrightarrow{GG}^,=\overrightarrow{AA}^,+\overrightarrow{CC^,}+\overrightarrow{BB}^,\)
ta đx biết nếu G là trọng tâm của ABC thì
GA+GB+GC=0
AA' =AG+GG'+G'A'
BB'=BG+GG'+G'B'
CC'=CG+GG'+G'C"
==> AA'+BB'+CC'=(AG+BG+CG)+3GG'+(G'A'+G'B'+G...
ĐPCM
dk cần và đủ để 2 tam giác có cùng trọng tâm là
AA'+BB'+CC' =0
c/m:
dk cần:AA'+BB'+CC'=0 thì ABC và A'B'C' cùng trọng tâm
vì AA'+BB'+CC'=3GG'
==> GG'=0 ==> G trùng G'
dk đủ: G trùng G' thì AA'+BB'+CC'=0
AA'+BB'+CC'=3GG'
mà GG' =0 ==> AA'+BB'+CC'=0 ĐPCM
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có đường cao AH. Gọi G là trọng tâm của tam giác ABC. Trên tai đối của tia HG lấy điểm E sao cho EH = HG. Tam giác ABC phải thỏa mãn điều kiện gì để tam giác GBE là tam giác đều ?
Ta có, tam giác AH là đường cao của tam giác cân ABC => góc AHB=90 độ=> góc BHE=90 độ
Xét tam giác BHG và tam giác BHE, ta có :
BH chung
GH= EH (gt)
góc AHB= góc BHE (=90 độ)
=> Tam giác BHG = Tam giác BHE
=> BG =BH ( cặp cạnh tương ứng )
=> Ta cần có GE = BG = BH thì tam giác BBE cân
Đúng 0
Bình luận (0)
bạn ơi vẽ hình nha để mìh giải gíup bạn nhanh hơn
Đúng 0
Bình luận (0)
Cho tam giác ABC cân ở A có đường phân giác AD (D thuộc BC) và đường trung tuyến BE (E thuộc AC) cắt nhau tại O
a) Chúng minh O là trọng tâm tam giác ABC
b) Tính độ dài OD biết AB = 5cm, BC = 8cm
c) Tam giác ABC cần có thêm điều kiện gì để O cũng là giao điểm 3 đường phân giác của tam giác ABC?
a) Xét ΔABD và ΔACD có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
Suy ra: BD=CD(hai cạnh tương ứng)
mà B,D,C thẳng hàng(gt)
nên D là trung điểm của BC
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC(cmt)
BE là đường trung tuyến ứng với cạnh BC(gt)
AD cắt BE tại O(gt)
Do đó: O là trọng tâm của ΔABC(Định lí ba đường trung tuyến của tam giác)
b) Ta có: D là trung điểm của BC(cmt)
nên \(BD=CD=\dfrac{BC}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Ta có: ΔABD=ΔACD(cmt)
nên \(\widehat{ADB}=\widehat{ADC}\)(hai góc tương ứng)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
Áp dụng định lí Pytago vào ΔABD vuông tại D, ta được:
\(AB^2=AD^2+BD^2\)
\(\Leftrightarrow AD^2=5^2-4^2=25-16=9\)
hay AD=3(cm)
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh CB(cmt)
O là trọng tâm của ΔABC(cmt)
Do đó: \(OD=\dfrac{1}{3}AD\)(Tính chất trọng tâm của tam giác)
hay OD=1(cm)
Vậy: OD=1cm
c) Xét ΔABC có
O là giao điểm của 3 đường phân giác
O là giao điểm của 3 đường trung tuyến
Do đó: ΔABC đều
Đúng 0
Bình luận (0)
Tam giác ABC có trọng tâm G, độ dài các cạnh BC, CA, AB lần lượt là a, b, c. Khi đó ABC là tam giác đều nếu có điều kiện nào sau đây? A.
a
G
A
→
+
b
G
B
→
+
c
G
C
→
0...
Đọc tiếp
Tam giác ABC có trọng tâm G, độ dài các cạnh BC, CA, AB lần lượt là a, b, c. Khi đó ABC là tam giác đều nếu có điều kiện nào sau đây?
A. a G A → + b G B → + c G C → = 0 →
B. a G A → + b G B → - c G C → = 0 →
C. a G A → - b G B → + c G C → = 0 →
D. - a G A → + b G B → + c G C → = 0 →
Cho tam giác ABC nhọn có ABAC, D và E theo thứ tự là trung điểm của AC và AB. Gọi G là trọng tâm tam giác ABC, M và N tương ứng là trung điểm của CG và BG1. Chứng minh MNDE là hình bình hành và MN + DE AB + AC2. Tìm điều kiện của tam giác ABC để MNDE là hình chữ nhật hoặc hình thoi3. Trên tia đối của tia DB lấy điểm K sao cho NK 5NB. Chung minh AK // BCGiúp mình nha, Thanks nhìu ^^
Đọc tiếp
Cho tam giác ABC nhọn có AB<AC, D và E theo thứ tự là trung điểm của AC và AB. Gọi G là trọng tâm tam giác ABC, M và N tương ứng là trung điểm của CG và BG
1. Chứng minh MNDE là hình bình hành và MN + DE < AB + AC
2. Tìm điều kiện của tam giác ABC để MNDE là hình chữ nhật hoặc hình thoi
3. Trên tia đối của tia DB lấy điểm K sao cho NK = 5NB. Chung minh AK // BC
Giúp mình nha, Thanks nhìu ^^
1: Xet ΔBCA có
E,D lần lượt là trung điểm của AB,AC
nên ED là đừog trung bình
=>ED//BC và ED=BC/2
Xét ΔGBC có
N,M lần lượt là trung điểm của GB,GC
nên NM là đường trung bình
=>NM//BC và NM=BC/2
=>ED//MN và ED=MN
=>EDMN là hình bình hành
MN+DE=BC/2+BC/2=BC<AB+AC
2 Để MNED là hình chữ nhật thì ED vuông góc EN
=>AG vuông góc BC
=>ΔABC cân tại A
=>AB=AC
3: NK=5NB
=>BK=6BN
=>BK=2BD
->D là trung điểm của BK
Xét tứ giác ABCK có
D là trung điểm chung của AC và BK
=>ABCK là hình bình hành
=>AK//BC
Đúng 1
Bình luận (1)
Cho tam giác ABC, M là trung điểm của BC. Điểm G là trọng tâm tam giác ABC nếu điều kiện nào dưới đây xảy ra?
A. G thuộc đường thẳng AM và GM = 1/2 GA
B. G thuộc tia MA và GA = 2/3 AM
C. G thuộc đoạn thẳng AM và MG = 2/3 AM
D. G thuộc tia MA và MG = 1/2 AG
Cho tam giác ABC có đường trung tuyến AM và trọng tâm G. Qua G kẻ đường thẳng song song với AB cắt BC tại H. Từ H kẻ đường thẳng song song song với AC cắt AB ở K. a) Tính tỉ số b) Tứ giác BKGH là hình gì? Vì sao? c) Tìm điều kiện của tam giác ABC để tứ giác BKGH là hình thoi? hình vuông?