Cho tam giác ABC có tâm đường tròn ngoại tiếp là I(3/2;1/16), tâm đường tròn nội tiếp là J(1;0). Phân giác trong góc A và phân giác ngoài góc B cắt nhau tại K(2;-8). tìm toạ độ A,B,C biết xB>0.
-->> help me !!!
Những câu hỏi liên quan
Cho tam giác ABC có M, N, P lần lượt là trung điểm ba cạnh BC, CA và AB. Tam giác MNP có
tâm đường tròn ngoại tiếp là J( 3;4) và trọng tâm G( 1;2) Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác ABC.
A.I(1;0) B.I(3; 2) C.I( 5;6) D.I( 2;3).
Cho tam giác ABC có A(-1; 1), B(3; 1), C(2; 4) . Tìm tọa độ điểm I là tâm đường tròn ngoại tiếp tam giác ABC.
A. I( 1; 2)
B. I(2; 1)
C. I(1; 1)
D. I(2; 2)
Chọn A.
Gọi I(x; y) là tâm đường tròn ngoại tiếp ΔABC
Suy ra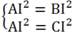 
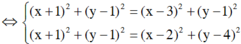
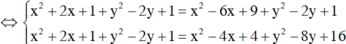
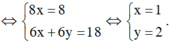
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc B=60, R=2, I là tâm đường tròn nội tiếp tam giác ABC. Tìm bán kính đường tròn ngoại tiếp tam giác AIC.
TOÁN 10. :)
cho tam giác ABC . lấy M trên AB, đường tròn ngoại tiếp tam giác BMC cắt AC tại N.
a, CMR AMN đồng dạng với ACB
b, I là tâm đường tròn ngoại tiếp tam giác AMN, CMR I thuộc 1 đường thẳng cố định
c, J là tâm đường tròn ngoại tiếp tam giác BMC. CMR IJ có độ dài ko đổi
Cho tam giác ABc , lấy D trên cạnh BC , vẽ đường tròn tâm I qua D tiếp xúc với AB tại B. Vẽ đường tròn tâm K qua D tiếp xúc với AC tại C . Gọi M là giao điểm của hai đường tròn đó
1. CM : tứ giác ABMC nội tiếp
2. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC . CM : 3 đường tròn tâm I, tâm K và tâm O đồng quy
3. CM : MD di chuyển qua 1 điểm cố định
Cho ba điểm A(4; 3), B(2; 7) và C(-3; -8).
a, Tìm tọa độ trọng tâm G và trực tâm H của tam giác ABC;
b, Gọi T là tâm đường tròn ngoại tiếp tam giác ABC. Chứng minh T, G và H thẳng hàng.
c, Viết phương trình đường tròn ngoại tiếp tam giác ABC.
a)
– Tọa độ trọng tâm G của tam giác ABC là:
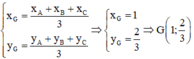
– Tọa độ trực tâm H của tam giác ABC:
Cách 1:
+ Phương trình đường cao BD:
BD ⊥ AC ⇒ Đường thẳng BD nhận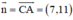 
là một vtpt
BD đi qua B(2; 7)
⇒ Phương trình đường thẳng BD: 7(x - 2) +11(y - 7) = 0 hay 7x + 11y – 91 = 0
+ Phương trình đường cao CE:
CE ⊥ AB ⇒ Đường thẳng CE nhận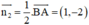 
là một vtpt
CE đi qua C(–3; –8)
⇒ Phương trình đường thẳng CE: 1(x + 3) – 2(y + 8)=0 hay x – 2y – 13 = 0.
Trực tâm H là giao điểm của BD và CE nên tọa độ của H là nghiệm của hpt:
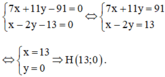
Cách 2: Gọi H(x, y) là trực tâm tam giác ABC
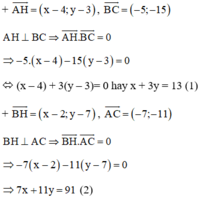
Từ (1) và (2) ta có hệ phương trình
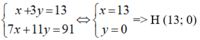
b) Gọi T(x; y) là tâm đường tròn ngoại tiếp tam giác ABC
Khi đó TA = TB = TC = R.
+ TA = TB ⇒ AT2 = BT2
⇒ (x – 4)2 + (y – 3)2 = (x – 2)2 + (y – 7)2
⇒ x2 – 8x + 16 + y2 – 6y + 9 = x2 – 4x + 4 + y2 – 14y + 49
⇒ 4x – 8y = –28
⇒ x – 2y = –7 (1)
+ TB = TC ⇒ TB2 = TC2
⇒ (x – 2)2 + (y – 7)2 = (x + 3)2 + (y + 8)2
⇒ x2 – 4x + 4 + y2 – 14y + 49 = x2 + 6x + 9 + y2 + 16y + 64
⇒ 10x + 30y = –20
⇒ x + 3y = –2 (2)
Từ (1) và (2) ⇒ x = –5, y = 1 ⇒ T(–5 ; 1).
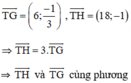
⇒ T, H, G thẳng hàng.
c) Tâm đường tròn ngoại tiếp ΔABC: T(–5; 1)
Bán kính đường tròn ngoại tiếp ΔABC:
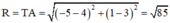
Vậy phương trình đường tròn ngoại tiếp tam giác ABC:
(x + 5)2 + (y – 1)2 = 85
Đúng 0
Bình luận (0)
cho tam giác ABC nhọn AB>AC ,nội tiếp đường tròn (O,R). có 3 đường cao AD, BE, CF cắt nhau tại H. Gọi I là tâm đường tròn ngoại tiếp tam giác AEF. a)CMR: HE.HB = 2HI.HD b) CM tứ giác DFIE nội tiếp và xác định tâm của đường tròn ngoại tiếp
cho tam giác ABC nhọn. M là trung điểm AC. kẻ MH vuông góc AB, H thuộc AB. I là tâm đường tròn ngoại tiếp tam giác ABC. N là trung điểm BC, P là trung điểm IN. chứng minh P là tâm đường tròn ngoại tiếp tam giác BCH.
cho tam giác ABC có AB=AC=40, BC=48. gọi O và I thứ tự là tâm đường tròn ngoại tiếp tam và nội tiếp tam giác. tính
a) Bán kính đường tròn nội tiếp
b) Bán kính đường tròn ngoại tiếp
c) Khoảng cách OI
Cho tam giác ABC có A=75 , C=45 và AC=a\(\sqrt{2}\) . Vẽ đường cao AK
a, Tính AB , KC theo a
b, Gọi H là trực tâm của tam giác ABC và O là tâm đường tròn ngoại tiếp tam giác ABC . Tính OHC
c, Gọi I là tâm đt nội tiếp tam giác ABC . Tính bán kính đt ngoại tiếp tam giác HOT theo a