cho tam giac ABC vuông tại B kéo dài đường trung tuyến AM lấy điểm D sao cho MD=MA.
So sánh CD với AB; CD với AC
So sánh GÓC BAM vỚI GÓC MAC
Những câu hỏi liên quan
cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a. Tính số đo góc ABD.
b. Chứng minh ΔABC = ΔBAD
c. So sánh độ dài AM và BCho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a. Xét ΔAMC và ΔBMD, ta có:
BM = MC (gt)
∠(AMB) = ∠(BMC) (đối đỉnh)
AM = MD (gt)
Suy ra: ΔAMC = ΔDMB (c.g.c)
⇒ ∠(MAC) = ∠D (2 góc tương ứng)
Suy ra: AC // BD
(vì có 2 góc ở vị trí so le trong bằng nhau)
Mà AB ⊥ AC (gt) nên AB ⊥ BD.
Vậy (ABD) = 90o.
b. Xét ΔABC và ΔBAD ta có:
AB cạnh chung
∠(BAC) = ∠(ABD) = 90o
AC = BD (vì ΔAMC = ΔDMB)
Suy ra: ΔABC = ΔBAD (c.g.c)
c. Ta có: ΔABC = ΔBAD ⇒ BC = AD (2 cạnh tương ứng)
Mặt khác: AM = 1/2 AD
Vậy AM = 1/2 BC.
Đúng 5
Bình luận (0)
a. Xét ΔAMC và ΔBMD, ta có:
BM = MC (gt)
∠(AMB) = ∠(BMC) (đối đỉnh)
AM = MD (gt)
Suy ra: ΔAMC = ΔDMB (c.g.c)
⇒ ∠(MAC) = ∠D (2 góc tương ứng)
Suy ra: AC // BD
(vì có 2 góc ở vị trí so le trong bằng nhau)
Mà AB ⊥ AC (gt) nên AB ⊥ BD.
Vậy (ABD) = 90o.
b. Xét ΔABC và ΔBAD ta có:
AB cạnh chung
∠(BAC) = ∠(ABD) = 90o
AC = BD (vì ΔAMC = ΔDMB)
Suy ra: ΔABC = ΔBAD (c.g.c)
c. Ta có: ΔABC = ΔBAD ⇒ BC = AD (2 cạnh tương ứng)
Mặt khác: AM = 1/2 AD
Vậy AM = 1/2 BC.
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. So sánh độ dài AM và BC.
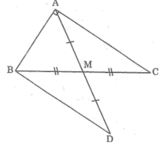
Ta có: ΔABC = ΔBAD ⇒ BC = AD (2 cạnh tương ứng)
Mặt khác: AM = 1/2 AD
Vậy AM = 1/2 BC.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuong tại B. Kéo dài trung tuyến AM lấy MD = MA
1, So sánh CD với AB , CD với AC
2, So sánh góc BMA với góc MAC
1)A)XÉT \(\Delta ABM\)VÀ\(\Delta DCM\)CÓ
\(BM=CM\left(GT\right)\)
\(\widehat{M_1}=\widehat{M_2}\left(Đ/Đ\right)\)
\(AM=DM\left(GT\right)\)
\(\Rightarrow\Delta ABM=\Delta DCM\left(C-G-C\right)\)
\(\Rightarrow AB=CD\)(HAI CẠNH TƯƠNG ỨNG)(1)
TA CÓ XÉT \(\Delta ABC\)VUÔNG TẠI B
\(\Rightarrow\widehat{B}>\widehat{C};\widehat{B}>\widehat{A}\)
VÌ\(\widehat{B}>\widehat{C}\)
\(\Rightarrow AB< AC\)QUAN HỆ GIỮA GÓC VÀ CẠNH ĐỐI DIỆN(2)
TỪ (1) VÀ (2) => \(AC>CD\)
B) CÂU B QUAN HỆ GIỮA CẠNH VÀ GÓC ĐỐI DIỆN
b) XÉT \(\Delta ADC\)
CÓ \(DC< AC\left(CMT\right)\)
\(\Rightarrow\widehat{ADC}>\widehat{DAC}\left(1\right)\)QUA HỆ GIỮA CẠNH VÀ GÓC ĐỐI DIỆN
MÀ \(\Delta ABM=\Delta DCM\left(CMT\right)\)
\(\Rightarrow\widehat{BAM}=\widehat{MDC}\)
HAY\(\widehat{BAM}=\widehat{ADC}\left(2\right)\)
TỪ (1) VÀ (2) \(\Rightarrow\widehat{BMA}>\widehat{MAC}\)
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA. Lấy điểm D sao cho MD = MA
a) Chứng minh :T/G AMC=T/G DMB
b) Chứng minh : T/G ABD vuông
c) Chứng minh : AD = BC
d) So sánh độ dài AM với BC , AB với BC ?
a: Xét ΔAMC và ΔDMB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)
MC=MB
Do đó: ΔAMC=ΔDMB
b: Ta có: ΔAMC=ΔDMB
nên \(\widehat{MAC}=\widehat{MDB}\)
mà hai góc này so le trong
nên AC//DB
hay DB⊥AB
=>ΔABD vuông tại B
c: Xét ΔCAB vuông tại A và ΔDBA vuông tại B có
BA chung
CA=DB
Do đó: ΔCAB=ΔDBA
Suy ra: AD=BC
d: AM=BC/2
AB<BC
Đúng 1
Bình luận (0)
Bài 1:Cho ABC vuông tại A, có AB = 3cm; AC = 4cm. Gọi AM là đường trung tuyến, trên tia đối của tia MA lấy điểm D sao cho AM = MD. a) Tính độ dài cạnh BC b) Chứng minh AB = CD, AB // CD c) Chứng minh góc BAM > góc CAM d) hạ AM vuông góc vs bc . Trên tia đối của tia ha lấy E sao cho HE=HA.cm DE SONG SONG BC
AI LÀM đc xong nhất là câu d) IB MIK nhận 20k thẻ cào nha
Cho tam giác ABC có AB AC, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD MA.a) Chứng minh AB CD, AB // CD.b) So sánh
M
A
B
^
và
M
A
C
^
.c) So sánh
A
M
B
^
và
A...
Đọc tiếp
Cho tam giác ABC có AB < AC, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh AB = CD, AB // CD.
b) So sánh M A B ^ và M A C ^ .
c) So sánh A M B ^ và A M C ^ .
Cho tam giác ABC vuông tại A, có AB = 3 cm, AC = 4 cm. Gọi AM là đường trung tuyến (M BC), trên tia đối của tia MA lấy điểm D sao cho AM = MD.
a) Tính dộ dài BC.
b) Chứng minh AB = CD, AB // CD.
c) Chứng minh góc BAM > góc CAM.
a, áp dụng định lí pytago vào tam giác ABC ta có:
\(BC^2=AB^2+AC^2\)
\(BC^2=3^2+4^2=25\)
\(BC=\sqrt{25}=5\)
B, xét tam giác BAC và DCA có:
BM=MC
AM=MD
góc BMA= DMC (đối đỉnh)
=> Tam giác BAC=DCA
=>BA=DC
Góc BAM=MDC=>BA//DC(so le trong)
cho mk xin **** nah
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, có AB = 3 cm, AC = 4 cm. Gọi AM là đường trung tuyến (M BC), trên tia đối của tia MA lấy điểm D sao cho AM = MD.
a) Tính dộ dài BC.
b) Chứng minh AB = CD, AB // CD.
c) Chứng minh góc BAM > góc CAM.
Cho tam giác ABC vuông tại A, có AB = 3 cm, AC = 4 cm. Gọi AM là đường trung tuyến (M BC), trên tia đối của tia MA lấy điểm D sao cho AM = MD.
a) Tính dộ dài BC.
b) Chứng minh AB = CD, AB // CD.
c) Chứng minh góc BAM > góc CAM.