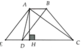
Câu 11.11. Tính diện tích hình thang ABCD, có đường cao bằng 12 cm, hai đường chéo AC và BD vuông góc với nhau, DB = 15 cm.
Câu 11.12. Hình thang cân ABCD có đáy lớn CD = 10 cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tìm đường cao của hình thang