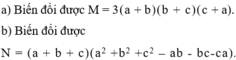ta có: ab(a + b) + bc(b + c) + ac(a + c) + 3abc 

= ab(a + b) + abc + bc(b + c) + abc + ac(a + c) + abc 

= ab(a + b + c) + bc(a + b + c) + ac(a + b + c) 

= (a + b + c)(ab + bc + ca) 

Ta có

a³+b³+c³-3abc

=(a+b)³-3ab(a+b)+c³-3abc

=[(a+b)³+c³]-3ab(a+b+c)

=(a+b+c)[(a+b)²-c(a+b)+c²]-3ab(a+b+c)

=(a=b+c)(a²+2ab+b²-ac-bc+c²)-3ab(a+b+c)

=(a+b+c)(a²+2ab+b²-ac-bc+c²-3ab)

=(a+b+c)(a²+b²+c²-ab-ac-bc)

a³+b³+c³-3abc

=(a+b)³-3ab(a+b)+c³-3abc

=[(a+b)³+c³]-3ab(a+b+c)

=(a+b+c)[(a+b)²-c(a+b)+c²]-3ab(a+b+c)

=(a=b+c)(a²+2ab+b²-ac-bc+c²)-3ab(a+b+c)

=(a+b+c)(a²+2ab+b²-ac-bc+c²-3ab)

=(a+b+c)(a²+b²+c²-ab-ac-bc)

a³ + b³ + c³ - 3abc

= [( a³ + b³ ) + c³ ] - 3abc

= [( a + b )³ + c³ + 3ab( a + b )] - 3abc

= [( a + b )³ + c³ ] + 3a²b + 3ab² - 3abc

= ( a + b + c ) [( a + b )² - c( a + b ) + c² ] - 3ab( a + b + c )

= ( a + b + c ) ( a² + 2ab + b² - ac - bc + c² - 3ab )

= ( a + b + c ) ( a² + b² + c² - ab - bc - ac )

= 1/2( a + b + c ) ( 2a² + 2b² + 2c² - 2ab - 2bc - 2ac )

= 1/2( a + b + c ) [( a² - 2ab + b² ) + ( a² - 2ac  + c² ) + ( b² - 2bc + c² )]

= 1/2 ( a + b + c ) [( a - b )² + ( a - c )² + ( b - c )²]

Hok Tốt!!!

Không phân tích được bạn nhé ^^

 Thay a^3+b^3=(a+b)^3 -3ab(a+b) .Ta có : 

Biến đổi vế trái thành: 

a^3+b^3+c^3-3abc 

<=>(a+b)^3 -3ab(a+b) +c^3 - 3abc 

<=>[(a+b)^3 +c^3] -3ab.(a+b+c) 

<=>(a+b+c). [(a+b)^2 -c.(a+b)+c^2] -3ab(a+b+c) 

<=>(a+b+c).(a^2+2ab+b^2-ca-cb+c^2-3ab 

<=>(a+b+c).(a^2+b^2+c^2-ab-bc-ca)

boc vai

\(a^3+b^3-c^3+3abc\)

\(=a^3+3ab.\left(a+b\right)+b^3-c^3-3abc-3ab.\left(a+b\right)\)

\(=\left(a+b\right)^3+c^3-3ab.\left(a+b-c\right)\)

\(=\left(a+b+c\right).\left(a^2+ab+b^2-ab-ac+c^2\right)-3ab.\left(a+b+c\right)\)

\(=\left(a+b+c\right).\left(a^2+b^2+c^2-ab-bc-ca\right)\)

Câu hỏi của Bắp Ngô - Toán lớp 8 - Học toán với OnlineMath

Tham khảo

a³+b³+c³-3abc=(a+b)³+c³-3a²b-3ab²-3abc

=(a+b+c)[(a+b)²-(a+b).c+c²]-3ab.(a+b+c)

=(a+b+c)(a²+b²+c²-ac-bc-ab)