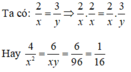
⇒ x2 = 64

⇒ x = 8 hoặc x = -8

Nếu x = 8 thì y = 96 : 8 = 12.

Nếu x = -8 thì y = 96 : (-8) = -12.

Từ \(\frac{2}{x}=\frac{3}{y}\)ta có :

\(\frac{4}{x^2}=\frac{2}{x}.\frac{3}{y}=\frac{6}{xy}=\frac{6}{96}=\frac{1}{6}\Rightarrow x=\pm8\)

Nếu x = 8 thì y = 96 : 8 = 12.

Nếu x = -8 thì y = 96 : (-8) = -12.

#)Giải :

Ta có : \(\frac{2}{x}=\frac{3}{y}\Rightarrow2y=3x\Rightarrow\frac{x}{2}=\frac{y}{3}\)

Đặt \(\frac{x}{2}=\frac{y}{3}=t\)

\(\Rightarrow x=2t;y=3t\)

\(\Rightarrow2t.3t=96\)

\(\Rightarrow t^2=16\Rightarrow\orbr{\begin{cases}t=4\\t=-4\end{cases}\Rightarrow\orbr{\begin{cases}x=-8;y=-12\\x=8;y=12\end{cases}}}\)

\(\Rightarrow\left(x,y\right)\in\left\{\left(-8,-14\right);\left(8,14\right)\right\}\)

Ta có : \(\frac{2}{x}=\frac{3}{y}\Rightarrow3x=2y\)\(\Rightarrow\frac{x}{2}=\frac{y}{3}\)

Đặt \(\frac{x}{2}=\frac{y}{3}=k\)\(\Rightarrow x=2k\)     ;        \(y=3k\)

Theo đề bài có : x.y = 96

\(\Rightarrow2k.3k=96\)  

        \(6k^2=96\)

\(\Rightarrow k^2=\frac{96}{6}=16\)

\(\Rightarrow\orbr{\begin{cases}k=\sqrt{16}=4\\k=-\sqrt{16}=-4\end{cases}}\)

\(\Rightarrow x=2k=2.4=8\)

     \(y=3k=3.4=12\)

\(\Rightarrow x=2.k=2.\left(-4\right)=-8\)

     \(y=3.k=3.\left(-4\right)=-12\)

Vậy có 2 cặp số x , y thỏa mãn là : x=8 ; y=12 và x=-8 ; y=-12

Mình nghĩ là làm thế này .

Ta có : ( y + 1 ) . ( xy - 1 ) = 3

=> ( y + 1 ) . ( x - 1 ) ( y - 1 ) = 3

=> [ ( y + 1 ) . ( y - 1 ) ] . ( x - 1 ) = 3

=> [ ( y . ( 1 - 1 ) ] . ( x - 1 ) = 3

=> 1 . ( x - 1 ) = 3

=> x - 1          = 3 : 1

=> x - 1          = 3

=> x               = 3 + 1

=> x               = 4

Vậy x = 4 ; y = 1

x - y = -658 y = 658 + x (1)

thế (1) vào xy = 1983, ta được:

x.(658 + x) = 1983
+ 658x - 1983 = 0
- 3x + 661x - 1983 = 0
( - 3x) + (661x - 1983) = 0
x(x - 3) + 661(x - 3) = 0
(x - 3)(x + 661) = 0

D

Ta có xy=2 ;yz=6;zx=3

=> xy.yz.zx=2.6.3 => (xyz)^2=36

*xyz=6 => z=3;x=1;y=2

*xyz=-6 => z=-3;x=-1 ;y=-2

Ta có: \(xy=2\Rightarrow y=\frac{2}{x}\left(1\right)\)

         \(yz=6\Rightarrow y=\frac{6}{z}\left(2\right)\)

Từ (1) và (2) \(\Rightarrow\frac{2}{x}=\frac{6}{z}\)

\(\Rightarrow\frac{x}{2}=\frac{z}{6}\)

Đặt \(\frac{x}{2}=\frac{z}{6}=k\Rightarrow\hept{\begin{cases}x=2k\\z=6k\end{cases}}\)

\(xz=3\Rightarrow2k\cdot6k=3\)

\(\Rightarrow12\cdot k^2=3\Rightarrow k^2=0,25\)

\(\Rightarrow k=0,5\)

\(x=2k\Rightarrow x=2\cdot0,5=1\)

\(z=6k\Rightarrow z=6\cdot0,5=3\)

Mà y=2/x => y=2:1=2

Vậy x=1; y=2;z=3

x=0

y=0

A, => x+2=0 hoặc y-3=0

=> x=-2 hoặc y=3

B, => x+1=0 hoặc xy-1=0

=> x=-1 hoặc xy=1

=> x=-1 hoặc x=y=+-1

a)  \(\left(x+2\right).\left(y-3\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x+2=0\\y-3=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-2\\y=3\end{cases}}\)

       vậy \(\orbr{\begin{cases}x=-2\\y=3\end{cases}}\)

b)  \(\left(x+1\right)\left(xy-1\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x+1=0\\xy-1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-1\\xy=1\end{cases}}\)

     vậy  \(\orbr{\begin{cases}x=-1\\xy=1\end{cases}}\)

a)Vì \(\left(x+2\right)\left(y-3\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x+2=0\\y-3=0\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=-2\\y=3\end{cases}}\)

b)Vì \(\left(x+1\right)\left(xy-1\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x+1=0\\xy-1=0\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=-1\\xy=1\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=-1\\-1.y=1\Leftrightarrow y=-1\end{cases}}\)