cho B=12/(2*4)^2+20/(4*6)^2+...+388/(96*98)^2+396/(98*100)^2. hãy so sánh B với 1/4

Những câu hỏi liên quan
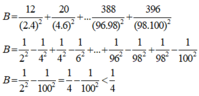
Cho B= 12 + 20 +...+ 388 +
(2×4)^2 (4×6)^2 (96×98)^2
396
(98×100)^2
Hãy so sánh B với 1
4
a. So sanh 2 phan so:A= 2015/2016+2016/2017+2017/2018 va B = 2015+2016+2017/2016+2017+2018
b.1/2.4+1/4.6+........+1/(2x-2).2x = 1/8
c.Cho A = 1/4+1/9+1/16+...+1/81+1/100 . Chung minh rang : A > 65/132
d.Cho B = 12/(2 . 4 ) ^ 2 + 20/ (4 . 6) ^2 + ...........+ 388/ ( 96 . 98 ) ^ 2 + 396/ ( 98 . 100 ) ^2 .Hay so sanh B voi 1 /4
B=12/(2×4)2+20/(4×6)2+...+396/(98×100)2
SO SÁNH B với 1/4
Ta có:
\(B=\frac{4^2-4^2}{\left(2\cdot4^2\right)}+\frac{6^2-4^2}{4^2\cdot4^2}+.....+\frac{98^2-96^2}{^{ }96^2\cdot98^2}+\frac{ }{ }\)\(\frac{100^2-98^2}{98^2\cdot100^2}\)
\(=\frac{1}{2^2}-\frac{1}{4^2}+\frac{1}{4^2}-\frac{1}{6^2}+.....+\frac{1}{96^2}-\frac{1}{98^2}-\)\(\frac{1}{100^2}\)
\(=\frac{1}{4}-\frac{1}{100^2}< \frac{1}{4}\)
Đúng 0
Bình luận (0)
Cho A=12/(2*4)2+20/(4*6)2+...+386/(96*98)2+988/(98*100)2
so sánh A với 1/4
Cho B=12/(2.4)^2+20/(4.6)^2+........+388/(96.98)^2+396/(98.100)^2. Hãy so sánh B với 1/4
) Cho B = 12/(2.4)2 + 20/(4.6)2 + … 388/(96.98)2 + 396/(98.100)2. Hãy so sánh B với 1/4
B=\(\frac{12}{2^2.4^2}+\frac{20}{4^2.6^2}+......+\frac{388}{96^2.98^2}+\frac{396}{98^2.100^2}\)
=\(\frac{1}{2^2}-\frac{1}{4^2}+\frac{1}{4^2}-\frac{1}{6^2}+...+\frac{1}{96^2}-\frac{1}{98^2}+\frac{1}{98^2}-\frac{1}{100^2}\)
=\(\frac{1}{2^2}-\frac{1}{100^2}\)
=\(\frac{2599}{10000}< \frac{2500}{10000}=\frac{1}{4}\)
=> B<\(\frac{1}{4}\)
Đúng 0
Bình luận (0)
Cho B = 12/(2.4)2 + 20/(4.6)2 + … 388/(96.98)2 + 396/(98.100)2. Hãy so sánh B với 1/4
Cho Bfrac{12}{left(2×4right)^2}+frac{20}{left(4×6^2right)}+.....+frac{388}{left(96×98right)^2}+frac{396}{left(98×100right)^2} So sánh B với frac{1}{4}
Đọc tiếp
Cho B=\(\frac{12}{\left(2×4\right)^2}\)+\(\frac{20}{\left(4×6^2\right)}\)+.....+\(\frac{388}{\left(96×98\right)^2}\)+\(\frac{396}{\left(98×100\right)^2}\) So sánh B với \(\frac{1}{4}\)
Cho
B
12
(
2.4
)
2
+
20
(
4.6
)
2
+
...
+
388
(
96.98
)
2
+...
Đọc tiếp
Cho B = 12 ( 2.4 ) 2 + 20 ( 4.6 ) 2 + ... + 388 ( 96.98 ) 2 + 396 ( 98.100 ) 2 . Hãy so sánh B với 1 4
B=\(\frac{12}{2^{2} . 4^{2}} + \frac{20}{4^{2} . 6^{2}} + . . . . . . + \frac{388}{9 6^{2} . 9 8^{2}} + \frac{396}{9 8^{2} . 10 0^{2}}\)
=\(\frac{1}{2^{2}} - \frac{1}{4^{2}} + \frac{1}{4^{2}} - \frac{1}{6^{2}} + . . . + \frac{1}{9 6^{2}} - \frac{1}{9 8^{2}} + \frac{1}{9 8^{2}} - \frac{1}{10 0^{2}}\)
=\(\frac{1}{2^{2}} - \frac{1}{10 0^{2}}\)
=\(\frac{2599}{10000} < \frac{2500}{10000} = \frac{1}{4}\)
=> B<\(\frac{1}{4}\)
Đúng 0
Bình luận (0)