Question

Cho B = 12 ( 2.4 ) 2 + 20 ( 4.6 ) 2 + ... + 388 ( 96.98 ) 2 + 396 ( 98.100 ) 2 . Hãy so sánh B với  1 4

Answer 1

Answer 2

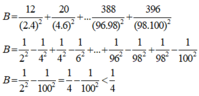
B=\(\frac{12}{2^{2} . 4^{2}} + \frac{20}{4^{2} . 6^{2}} + . . . . . . + \frac{388}{9 6^{2} . 9 8^{2}} + \frac{396}{9 8^{2} . 10 0^{2}}\)

   =\(\frac{1}{2^{2}} - \frac{1}{4^{2}} + \frac{1}{4^{2}} - \frac{1}{6^{2}} + . . . + \frac{1}{9 6^{2}} - \frac{1}{9 8^{2}} + \frac{1}{9 8^{2}} - \frac{1}{10 0^{2}}\)

   =\(\frac{1}{2^{2}} - \frac{1}{10 0^{2}}\)

   =\(\frac{2599}{10000} < \frac{2500}{10000} = \frac{1}{4}\)

     => B<\(\frac{1}{4}\)