giải phương trình
\(x+\frac{2a|x+a|}{x}=\frac{a^2}{x}\)( a là hằng số)
Những câu hỏi liên quan
Giải phương trình
\(\frac{x+a}{x+2}+\frac{x-2}{x-a}=2\) (a là hằng số)
ĐKXĐ: \(x\ne a;x\ne-2\)
PT\(\Leftrightarrow\frac{\left(x+a\right)\left(x-a\right)}{\left(x+2\right)\left(x-a\right)}+\frac{\left(x-2\right)\left(x+2\right)}{\left(x+2\right)\left(x-a\right)}=2\)
\(\Rightarrow\left(x+a\right)\left(x-a\right)+\left(x-2\right)\left(x+2\right)=2\left(x+2\right)\left(x-a\right)\)
\(\Leftrightarrow x^2-a^2+x^2-4=2\left(x^2+2x-ax-2a\right)\)
\(\Leftrightarrow2x^2-a^2-4=2x^2+4x-2ax-4a\)
\(\Leftrightarrow-a^2-4=\left(4-2a\right)x-4a\)
\(\Leftrightarrow\left(2a-4\right)x=a^2-4a+4\)
\(\Leftrightarrow2\left(a-2\right)x=\left(a-2\right)^2\)
Nếu a=2 thì PT có vô số nghiệm khác 2 và -2
Nếu a khác 2 thì PY có 1 nghiệm \(x=\frac{a-2}{2}\)với ĐK \(\hept{\begin{cases}\frac{a-2}{2}\ne-2\\\frac{a-2}{2}\ne a\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a-2\ne-4\\a-2\ne2a\end{cases}}\)
\(\Leftrightarrow a\ne-2\)
Vậy nếu a=2 thì PT có vô số nghiệm khác \(\pm\)2.Nếu a \(\ne\pm\)2 thì PT có 1 nghiệm \(x=\frac{a-2}{2}\).Nếu a=-2 thì PT vô nghiệm.
Đúng 0
Bình luận (0)
Giải phương trình 2 x a − x−2a 3a a là hằng số
giải phương trình : \(\frac{1}{\left(x+a\right)^2-1}+\frac{1}{\left(x+1\right)^2-a^2}=\frac{1}{x^2-\left(a+1\right)^2}+\frac{1}{x^2-\left(a-1\right)^2}\)( a là hằng số)
Cho phương trình: \(\frac{3a+1}{a+x}-\frac{a-1}{a-x}=\frac{2a\left(a^2-1\right)}{x^2-a^2}\)( với a là tham số )
a, Giải phương rình trên.
b, Tìm các giá trị nguyên dương của a để phương trình có nghiệm x là số nguyên tố
Giải phương trình:
\(\frac{x-a}{a+b}+\frac{x-b}{a-b}=\frac{2ab}{b^2-a^2}\) (a và b là hằng).
Điều kiện xác định của phương trình: \(a\ne\pm b\)
Biến đổi phương trình:
(x - a)(a - b) + (x - b)(a + b) = - 2ab
<=> ax - bx - a2 + ab + ax + bx - ab - b2 = - 2ab
<=> 2ax = a2 + b2 - 2ab
<=> 2ax = (a - b)2 (1)
Nếu \(a\ne0\) thì \(x=\frac{\left(a-b\right)^2}{2a}\)
Nếu a = 0 thì (1) có dạng 0x = b2. Do \(a\ne b\) nên \(b\ne0\)nên phương trình vô nghiệm.
Kết luận:
Nếu \(\hept{\begin{cases}a\ne b\\a\ne\pm b\end{cases}}\) thì \(S=\left\{\frac{\left(a-b\right)^2}{2a}\right\}\)
Còn lại, \(S=\varnothing\)
Đúng 0
Bình luận (0)
GPT
a) \(\frac{x}{2a+x}+\frac{2a+x}{2a-x}=\frac{8a^2}{x^2-4a^2}\)(a là hằng)
b) \(\frac{2a-3b}{x-2a}+\frac{3b-2a}{x-3b}=0\)(a và b là hằng)
giải bất phương trình : \(\frac{2x}{a^2-a+1}-\frac{1}{2a+a}< \frac{4x-1}{2a^2-2a+2}+\frac{a-2ax}{1+a^3}\)(a là hằng số)
Giải bất phương trình với a là hằng số x + 1 a + a x > x + 2 a - 2 x
Điều kiện xác định: a ≠ 0.
Ta có: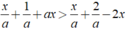
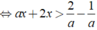
⇔ x( a + 2 ) > 1/a ( 1 )
+ Nếu a > - 2,a ≠ 0 thì nghiệm của bất phương trình là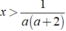
+ Nếu a < - 2 thì nghiệm của bất phương trình là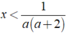
+ Nếu x = - 2 thì ( 1 ) có dạng 0x > - 1/2 luôn đúng với ∀ x ∈ R
Đúng 0
Bình luận (0)
Giải bất phương trình sau với a là hằng số:
\(\frac{2x}{a^2-a+1}-\frac{1}{2a+2}< \frac{4x-1}{2a^2-2a+2}+\frac{a-2ax}{1+a^3}\)
Trước hết xoá \(\frac{2x}{a^2-a+1}\)ở 2 vế. Nếu \(\frac{a}{a+1}>0\left(a< -1;a>0\right)\)thì \(x< \frac{a}{4}\). Nếu \(\frac{a}{a+1}< 0\left(-1< a< 0\right)\)thì \(x>\frac{a}{4}\)
\(ĐKXĐ:a\ne-1\)
\(\frac{2x}{a^2-a+1}-\frac{1}{2a+2}< \frac{4x-1}{2a^2-2a+2}+\frac{a-2ax}{1+a^3}\Leftrightarrow\frac{2x}{a^2-a+1}-\frac{1}{2a+2}< \frac{2x}{a^2-a+1}-\frac{1}{2a^2-2a+2}+\frac{a}{1+a^3}-\frac{2ax}{1+a^3}\)\(\Leftrightarrow\frac{1}{2a+2}-\frac{1}{2a^2-2a+2}+\frac{a}{1+a^3}>\frac{2ax}{1+a^3}\Leftrightarrow\frac{a^2-a+1-a-1+2a}{2\left(a^3+1\right)}>\frac{2ax}{1+a^3}\Leftrightarrow\frac{a^2}{2\left(1+a^3\right)}>\frac{4ax}{2\left(1+a^3\right)}\)\(\Leftrightarrow\frac{4ax}{a+1}< \frac{a^2}{a+1}\)
* Nếu \(\frac{a}{a+1}>0\)(tức là a < -1 hoặc a > 0) thì \(x< \frac{a}{4}\)
* Nếu \(\frac{a}{a+1}< 0\)(tức là -1 < a < 0) thì \(x>\frac{a}{4}\)
?????????????????????????