Điều kiện xác định: a ≠ 0.
Ta có: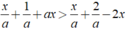
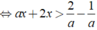
⇔ x( a + 2 ) > 1/a ( 1 )
+ Nếu a > - 2,a ≠ 0 thì nghiệm của bất phương trình là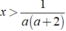
+ Nếu a < - 2 thì nghiệm của bất phương trình là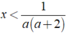
+ Nếu x = - 2 thì ( 1 ) có dạng 0x > - 1/2 luôn đúng với ∀ x ∈ R
Điều kiện xác định: a ≠ 0.
Ta có: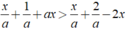
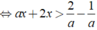
⇔ x( a + 2 ) > 1/a ( 1 )
+ Nếu a > - 2,a ≠ 0 thì nghiệm của bất phương trình là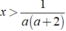
+ Nếu a < - 2 thì nghiệm của bất phương trình là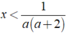
+ Nếu x = - 2 thì ( 1 ) có dạng 0x > - 1/2 luôn đúng với ∀ x ∈ R
Giải bất phương trình sau với a là hằng: \(2\left(x+2\right)< a\left(a-x\right)\)
Giải bất phương trình với a,b là các hằng số( a khác 0).
\(\frac{ax-b}{a}+(a+b+1)x>\frac{2b}{a}\)
Giải phương trình
1. x^3 - 7x^2 + 15x - 25
2. x(x + 3) + a(a - 3) = 2(ax - 1) với a là hằng số
3. x^3 + (x + 1)^3 + (x + 2)^3 = (x + 3)^3
Giải phương trình 2 x a − x−2a 3a a là hằng số
cho biết a là hằng số giải phương trình sau
x (x+3) + a (a-3) = 2 (ax-1)
Cho biêt a là hằng số. giải các phương trình sau:
a) x(x+3) +a(a-3) =2(ax-1)
b) x^2+7x-a^2+a+12=0
Giải phương trình
\(\frac{x+a}{x+2}+\frac{x-2}{x-a}=2\) (a là hằng số)
giải phương trình với a,b là hằng số : a.(ax+b)=b2.(x-1)
giải phương trình
1) 1/a+b+c=1/a +1/b +1/x (a,b là hằng số; a,b khác 0)
2)1/(x+a)2-1 +1/(x+1)2-a2 = 1/x2-(a+1)2 +1/x2-(a-1)2 (a là hằng số)