tìm các giá trị nguyên của n để 3n - 1 chia hết cho n-1

Những câu hỏi liên quan
Tìm giá trị nguyên của n
a/ 7 chia hết cho n+2
b/ n+1 chia hết cho n-3
c/ Để giá trị của biểu thức \(3n^3+10n^2-5\) chia hết cho giá trị của biểu thức 3n+1
d/ Để giá trị của biểu thức \(10n^2+n-10\) chia hết cho giá trị của biểu thức n-1
a: =>\(n+2\in\left\{1;-1;7;-7\right\}\)
=>\(n\in\left\{-1;-3;5;-9\right\}\)
b: =>n-3+4 chia hết cho n-3
=>\(n-3\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{4;2;5;1;7;-1\right\}\)
c: =>3n^3+n^2+9n^2-1-4 chia hết cho 3n+1
=>\(3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{0;-\dfrac{2}{3};\dfrac{1}{3};-1;1;-\dfrac{5}{3}\right\}\)
d: =>10n^2-10n+11n-11+1 chia hết cho n-1
=>\(n-1\in\left\{1;-1\right\}\)
=>\(n\in\left\{2;0\right\}\)
Đúng 1
Bình luận (0)
Tìm các giá trị nguyên của n để 3n+2 chia hết cho n-1
Ta có :
\(3n+2=3n-3+5=3.\left(n-1\right)+5\)chia hết cho \(n-1\)\(\Rightarrow\)\(5\)chia hết cho \(n-1\)\(\Rightarrow\)\(\left(n-1\right)\inƯ\left(5\right)\)
Mà \(Ư\left(5\right)=\left\{1;-1;5;-5\right\}\)
Do đó :
\(n-1=1\Rightarrow n=1+1=2\)
\(n-1=-1\Rightarrow n=-1+1=0\)
\(n-1=5\Rightarrow n=5+1=6\)
\(n-1=-5\Rightarrow n=-5+1=-4\)
Vậy \(n\in\left\{2;0;6;-4\right\}\)
Đúng 0
Bình luận (0)
Ta có :3n+2=3n-3+3+2
=3(n-1)+5 do 3(n-1)chia hết cho n-1 ,để cho 3n+2 chia hết cho n-1
suy ra 5chia hết cho n-1 do n là số nguyên
suy ra n-1 thuộc 1;-1;5;-5
suy ra n thuộc 2;0;6;-4
Vậy n thuộ 2; 0; 6; -4
Đúng 0
Bình luận (0)
Tìm các giá trị nguyên của n để 2n^2+3n+3 chia hết cho giá trị của biểu thức 2n-1
Tìm các giá trị nguyên của n để biểu thức 6n-3 chia hết cho 3n+1
Ta có: 6n-3 chia hết cho 3n+1
<=> (6n + 2 )- 5 chia hết 3n + 1
<=> 2.(3n + 1) - 5 chia hết 3n + 1
=> 5 chia hết 3n + 1
=> 3n + 1 E Ư(5) = {-1;1;-5;5}
Ta có:
| 3n + 1 | -1 | 1 | -5 | 5 |
| 3n | -2 | 0 | -6 | 4 |
| n | ? | 0 | -2 | ? |
Đúng 0
Bình luận (0)
Tìm giá trị nguyên của n
a/ Để giá trị của biểu thức 3n3 + 10n2 – 5 chia hết cho giá trị của biểu thức 3n+1.
b/ Để giá trị của biểu thức 10n2 + n – 10 chia hết cho giá trị của biểu thức n – 1 .
a) Cho 3n +1=0 => n=\(\frac{-1}{3}\)
Sau đó thay vào biểu thức 3n3+10n2-5 sẽ tìm ra n=-4
b) Cho n-1=0 => n=1
Sau đó thay vào biểu thức 10n2+n -10 sẽ tìm ra n=1
Cho mình nha!!! <3
Đúng 0
Bình luận (0)
tìm các giá trị nguyên của n để giá trị của biểu thức
a) n3-2n+3n+3 chia hết cho giá trị của biểu thức n-1
b) 10n2+n-10 chia hết cho giá trị của biểu thức n-4
Ta có : n3 - 2n + 3n + 3
= n3 - n + 3
= n(n2 - 1)
= n(n - 1)(n + 1) + 3
Để n3 - 2n + 3n + 3 chia hết cho n - 1
=> n(n - 1)(n + 1) + 3 chia hết cho n - 1
=> 3 chia hết cho n - 1
=> n - 1 thuộc Ư(3) = {-3;-1;1;3}
=> n = {-2;0;2;4}
Đúng 0
Bình luận (0)
Tìm giá trị nguyên của n để giá trị của biểu thức 3n*3 + 10n*2 - 5 chia hết cho 3n+1
A = (3n^3 + 10n^2 - 5)/(3n + 1)
A = (3n^3 + n^2 + 9n^2 + 3n - 3n - 1 -4)/(3n+1)
A= n^2 + 3n - 1 - 4/(3n+1)
biểu thức 3n^3 + 10n^2 - 5 chia hết cho giá trị của biểu thức 3n + 1 khi:
3n+1 = ±1,±2, ±4
=> n = 0,-2/3,1/3,-1,1,-5/3
chọn giá trị nguyên: n = 0,-1,1
CHÚC BẠN HỌC TỐT
Đúng 0
Bình luận (0)
\(A=\frac{\left(3n^3+10n^2-5\right)}{\left(3n+1\right)}\)
\(A=\frac{\left(3n^3+n^2+9n^2+3n-3n-1-4\right)}{\left(3n+1\right)}\)
\(A=\frac{n^2+3n-1-4}{\left(3n+1\right)}\)
Biểu thức \(3n^3+10n^2-5\)chia hết cho giá trị của biểu thức \(3n+1\) khi:
3n+1 = ±1,±2, ±4
\(\Rightarrow n=0;-\frac{2}{3};-\frac{1}{3};-1;-\frac{5}{3}\)
Chọn giá trị nguyên:\(n=0;-1;1\)
Đúng 0
Bình luận (0)
A = (3n^3 + 10n^2 - 5)/(3n + 1)
A = (3n^3 + n^2 + 9n^2 + 3n - 3n - 1 -4)/(3n+1)
A= n^2 + 3n - 1 - 4/(3n+1)
biểu thức 3n^3 + 10n^2 - 5 chia hết cho giá trị của biểu thức 3n + 1 khi:
3n+1 = ±1,±2, ±4
=> n = 0,-2/3,1/3,-1,1,-5/3
Đúng 0
Bình luận (0)
Bài 6: Tìm giá trị nguyên của n để :
1) 3n^3 +10n^2 - 5 chia hết cho 3n+1
2) 4n^3 +11n^2 +5n+ 5 chia hết cho n+2
3) n^3 - 4n^2 +5n -1 chia hết cho n-3
1: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;4;2;-2;-1;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;3;-3\right\}\)
hay \(n\in\left\{0;1;-1\right\}\)
Đúng 0
Bình luận (0)
Tìm giá trị nguyên của n để giá trị biểu thức 3 n 3 + 10 n 2 - 5 chia hết cho giá trị của biểu thức 3n + 1
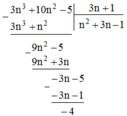
Ta có: 3 n 3 + 10 n 2 - 5 = 3 n + 1 n 2 + 3 n - 1 - 4
Để phép chia đó là chia hết thì 4 ⋮ 3n + 1⇒ 3n + 1 ∈ Ư(4)
3n + 1 ∈ {-4; -2; -1; 1; 2; 4}
3n + 1 = -4⇒ 3n = -5⇒ n = 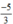 ∉ Z : loại
∉ Z : loại
3n + 1 = -2⇒ 3n = -3⇒ n = -1 ∈ Z
3n + 1 = -1⇒ 3n = -2⇒ n = 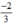 ∉ Z : loại
∉ Z : loại
3n + 1 = 1⇒ 3n = 0⇒ n = 0 ∈ Z
3n + 1 = 2⇒ 3n = 2⇒ n = 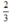 ∉ Z : loại
∉ Z : loại
3n + 1 = 4⇒ 3n = 3⇒ n = 1 ∈ Z
Vậy n ∈ {-1; 0; 1} thì 3 n 3 + 10 n 2 - 5 chia hết cho 3n + 1.
Đúng 1
Bình luận (0)























