Bạn tra gu gồ được mà,hỏi làm gì cho mệt chớ,tìm được cách làm trên gu gồ là áp dụng vào bài thôi

 noi A vs C ,BvsC

ap dung tinh chat duong trug binh cua tam giac

AM=EN

MN=FE

MNEF la hinh thoi

Đáp án A

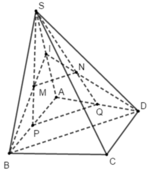
+) M là trọng tâm của tam giác SAB nên giao điểm P của SM và AB là trung điểm của AB.

Suy ra SM = 2/3 SP ⇒ S M S P = 2 3

N là trọng tâm của tam giác SAD nên giao điểm Q của SN và AD là trung điểm của AD

Suy ra SN = 2/3 SQ ⇒ S N S Q = 2 3

Xét tam giác SPQ có   S M S P = S N S Q = 2 3  nên MN // PQ (1) (định lý Ta-lét)

Do đó đáp án A đúng.

+) Xét tam giác IBD có

I M I B = 1 3 (tam giác SAB có I là trung điểm của SA và M là trọng tâm)

I N I D = 1 3  (tam giác SAD có I là trung điểm của SA và N là trọng tâm)

Do đó I M I B = I N I D = 1 3  nên MN // BD

Suy ra đáp án B, C, D sai.

Chọn đáp án A

Nối BC và AD kéo dài cắt nhau tại F

\(\Rightarrow SF=\left(SBC\right)\cap\left(SAD\right)\)

Trong mp (SCD), nối CM kéo dài cắt SD tại G

\(\Rightarrow AG=\left(AMC\right)\cap\left(SAD\right)\)

Trong mp (SCD), nối SM kéo dài cắt CD tại E

\(\Rightarrow AE=\left(SAM\right)\cap\left(ABCD\right)\)

Trong mp (ABCD), nối BE cắt AC tại H

\(\Rightarrow SH=\left(SBM\right)\cap\left(SAC\right)\)

Ta có : Tứ giác MPNQ là hình bình hành

$\Rightarrow$ MN và PQ cắt nhau tại trung điểm I của mỗi đường

Ta có : Tứ giác EPFQ là hình bình hành

$\Rightarrow$ EF đi qua I

Vậy EF , MN và PQ đồng quy