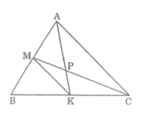
Xét △ PAC và  △ PKM,ta có:

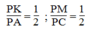
Suy ra: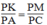 

Lại có: ∠ (APC) =  ∠ (KPM) (đối đỉnh)

Suy ra:  △ PKM đồng dạng  △ PAC(c.g.c) với tỉ số đồng dạng k = 1/2

Suy ra: 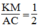 (1)

Vì  △ PKM đồng dạng △ PAC nên  ∠ (PKM) =  ∠ (PAC)

Suy ra: KM //AC (vì có cặp góc ở vị trí so le trong bằng nhau)

Trong  △ ABC, ta có: KM // AC

Suy ra:  △ BMK đồng dạng  △ BAC (g.g)

Suy ra: 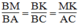 (2)

Từ 1 và (2) suy ra: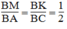 

Vì BM = 1/2 BA nên M là trung điểm AB.

Vì BK = 1/2 BC nên K là trung điểm BC.

Cho mình xin hình!

BẠN PHẢI TỰ VẼ

BẠN NHÌN KĨ PHẦN A ĐI

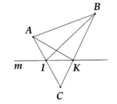
a) Vì hai điểm A, B nằm trên hai nửa mặt phẳng đối nhau bờ m nên đoạn thẳng AB cắt đường thẳng m.

b) Từ câu a), ta suy ra điểm K nằm giữa hai điểm B, C  nên tia AK nằm giữa hai tia AB và AC.

Tương tự, ta có điểm I nằm giữa hai điểm A, C nên tia BI nằm giữa, hai tia BA, BC.

c*) Từ câu b), ta suy ra tia BI nằm giữa hai tia BA,BK nên tia BI cắt đoạn thẳng AK tại một điểm nằm giữa A và K.

Lập luận tương tự, ta có tia AK cắt đoạn thẳng BI tại một điểm nằm giữa B và I. Từ đó suy ra hai đoạn thẳng AK và BI cắt nhau.

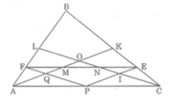
Gọi Q là giao điểm của PF và AK ,I là giao điểm của PE và CL

Trong △ FPE ta có: PE//AK hay QM //PE

Suy ra: 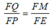 (định lí ta-lét) (1)

Trong  △ ALO ta có:PF //CL hay FQ //LO

Suy ra: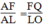 (định lí ta-lét) (2)

Trong  △ ALC ta có: PF // CL

Suy ra: 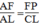 (định lí ta-lét) (3)

Từ (2) và (3) suy ra: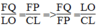 

Vì LO = 1/3 CL (O giao điểm của hai đường trung tuyến) nên 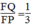 (4)

Từ (1) và (4) suy ra:  ⇒ FM = 1/3 FE

Trong  △ EPF ta có:PF // CL hay NI // PF

Suy ra:  (định lí ta –lét) (5)

Trong  △ CKO ta có: EI // OK

Suy ra: 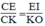 (định lí ta –lét) (6)

Trong  △ CKA ta có:PE // AK

Suy ra: 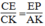 (định lí ta –lét) (7)

Từ (6) và (7) suy ra: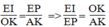 

Vì OK = 1/3 AK (O là giao điểm của hai đường trung tuyến) nên 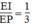 (8)

Từ (5) và (8) suy ra: 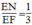 ⇒EN = 1/3 EF

Ta có: MN = EF - (EN + FM) = EF - (1/3 EF + 1/3 EF) = 1/3 EF

Vậy EN = MN = NF