Cho hình thang ABCD có đường chéo vuông góc với cạnh bên. kẻ đường caoAH biếtDH=5;CH=15
a, tính độ dài 2 đường chéo
b,tính đường cao AH
C, tính diện tích của hình thang ABCD
Cho hình thang cân ABCD, đáy lớn CD=10cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tính đường cao của hình thang cân
Gợi ý: Kẻ BK vuông góc với CD
Kẻ AH⊥BC, BK⊥CD, đường chéo AC⊥AD
Đặt HC=HK+CK=x+\(\dfrac{10-x}{2}\)=\(\dfrac{x+10}{2}\)
Áp dụng hệ thức lượng trong ΔADC⊥A
Có
Cho hình thang cân ABCD có đáy lớn gấp hai lần đáy bé và đáy lớn bằng tổng 2 cạnh bên.
a, Tính các góc của hình thang ABCD
b, Tính góc hợp bởi 2 đường chéo
c, Chứng minh đường chéo vuông góc với cạnh bên
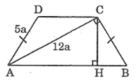
Cho hình thang ABCD có hai cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 5a, AC = 12a
Tính chiều cao của hình thang ABCD
Cho hình thang cân ABCD có đáy lớn 𝐶𝐷 = 10𝑐𝑚, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tính diện tích hình thang cân đó.
Kẻ đường cao góc AE \(\Rightarrow AE=AB\)
Lại có ABCD là hình thang cân \(\Rightarrow CD=AB+2DE=AE+2DE\Rightarrow DE=\dfrac{CD-AE}{2}=\dfrac{10-AE}{2}\)
\(EC=AB+DE=AE+DE=AE+\dfrac{10-AE}{2}=\dfrac{AE+10}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông ACD có:
\(AE^2=DE.EC\Leftrightarrow AE^2=\left(\dfrac{10-AE}{2}\right)\left(\dfrac{10+AE}{2}\right)\)
\(\Leftrightarrow4AE^2=100-AE^2\Rightarrow AE=2\sqrt{5}\) \(\Rightarrow AB=2\sqrt{5}\)
\(S_{ABCD}=\dfrac{1}{2}AE.\left(AB+CD\right)=\dfrac{1}{2}.2\sqrt{5}.\left(2\sqrt{5}+10\right)=...\)
Hình thang ABCD có đáy lớn CD = 10, đáy nhỏ = đường cao, đường chéo vuông góc với cạnh bên. Tính đường cao hình thang.
Câu 11.11. Tính diện tích hình thang ABCD, có đường cao bằng 12 cm, hai đường chéo AC và BD vuông góc với nhau, DB = 15 cm.
Câu 11.12. Hình thang cân ABCD có đáy lớn CD = 10 cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tìm đường cao của hình thang
Câu 11.12.
Kẻ đường cao \(AH,BK\).
Do tam giác \(\Delta AHD=\Delta BKC\left(ch-gn\right)\)nên \(DH=BK\).
Đặt \(AB=AH=x\left(cm\right),x>0\).
Suy ra \(DH=\frac{10-x}{2}\left(cm\right)\)
Xét tam giác \(AHD\)vuông tại \(H\):
\(AD^2=AH^2+HD^2=x^2+\left(\frac{10-x}{2}\right)^2\)(định lí Pythagore)
Xét tam giác \(DAC\)vuông tại \(A\)đường cao \(AH\):
\(AD^2=DH.DC=10.\left(\frac{10-x}{2}\right)\)
Suy ra \(x^2+\left(\frac{10-x}{2}\right)^2=10.\frac{10-x}{2}\)
\(\Leftrightarrow x=2\sqrt{5}\)(vì \(x>0\))
Vậy đường cao của hình thang là \(2\sqrt{5}cm\).
Câu 11.11.
Kẻ \(AE\perp AC,E\in CD\).
Khi đó \(AE//BD,AB//DE\)nên \(ABDE\)là hình bình hành.
Suy ra \(AE=BD=15\left(cm\right)\).
Kẻ đường cao \(AH\perp CD\)suy ra \(AH=12\left(cm\right)\).
Xét tam giác \(AEC\)vuông tại \(A\)đường cao \(AH\):
\(\frac{1}{AH^2}=\frac{1}{AE^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AE^2}=\frac{1}{12^2}-\frac{1}{15^2}=\frac{1}{400}\)
\(\Rightarrow AC=20\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.15.20=150\left(cm^2\right)\),
Cho hình thang ABCD vuông tại A có cạnh đáy AB bằng 6cm, cạnh bên AD bằng 4cm và hai đường chéo vuông góc với nhau. Tính độ dài các cạnh DC, CB và đường chéo DB.
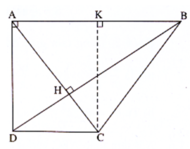
Hai đường chéo AC, BD cắt nhau tại H. Trong tam giác vuông ABD, ta có:
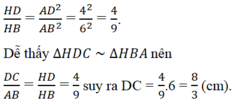
Kẻ đường cao CK của tam giác ABC, dễ thấy KB = AB – DC = 6 - 8/3 = 10/3.
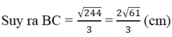
Tam giác vuông ABD có D B 2 = A B 2 + A D 2 = 6 2 + 4 2 = 52, từ đó DB = 52 = 2 13 (cm)
Cho hình thang ABCD có AB//CD, AB<CD, đường chéo BD vuông góc với cạnh BC. Kẻ BH vuông góc với CD. Tính diện tích hình thang ABCD biết BC=15cm, DC= 25cm. (ABCD ko phải hình thang cân)
cho hình thang cân ABCD có đường chéo BD vuông góc với cạnh bên BC, BD là tia phân giác góc D, BC=6cm. Tính chu vi hình thang ABCD
ABCD là hình thang cân (gt) nên AB song song với CD,AD=BC=6cm và góc C=góc ADC
DB la tia p/g của góc ADC(gt) nên góc ADB=góc BDC= 1/2 góc ADC =1/2 góc C
AB song song với CD (cmt) suy ra: góc ABD=góc BDC
Tam giác ABD có: góc ABD=góc ADB(=góc BDC)
Do đó tam giác ABD cân tại A (DHNB) suy ra: AB=AD=6cm
Tam giác DBC vuông tại B nên góc BDC+góc C=90 độ
Hay 1/2 góc C+ góc C=90 độ
3/2 góc C =90 độ
C=60 độ.Sau đó tính được góc BDC=30 độ
Tam giác BDC vuông tại B có góc BDC=30 độ vì thế BC=1/2 DC
Do đó:DC=2BC=2x6=12(cm)
Chu vi hình thang ABCD là:
AB+AD+BC+CD=6+6+6+12=30(cm)
Vậy chu vi hình thang ABCD là 30 cm