Cho tam giác ABC có góc B = góc C . Tia phân giác của góc A cắt BC tại D. Chứng minh rằng BD=DC;AB=AC

Những câu hỏi liên quan
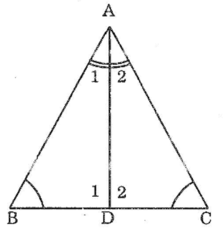
Cho tam giác ABC có ∠B =∠C Tia phân giác của góc A cắt BC tại D. chứng minh rằng: BD = DC; AB = AC
Trong ΔADB, ta có:
∠B +∠(A1 ) +∠(D1) =180o (tổng 3 góc trong tam giác)
Suy ra: ∠(D1 ) =180o-(∠B +(A1)) (1)
Trong ΔADC, ta có:
∠C +∠(A2) +∠(D2) =180o (tổng 3 góc trong tam giác)
Suy ra: ∠(D2) =180o-(∠C +∠(A2) ) (2)
+) Lại có: ∠B =∠C (gỉa thiết)
∠(A1 ) =∠(A2) (vì AD là tia phân giác của góc BAC) (3)
Từ (1), (2) và (3) suy ra: ∠(D1) =∠(D2)
Xét ΔABD và ΔACD, ta có:
∠(A1 ) =∠(A2) ( Vì AD là tia phân giác của góc BAC)
AD cạnh chung
∠(D1 ) =∠(D2) ( chứng minh trên).
Vậy: ΔABD= ΔACD (g.c.g)
Vậy: AB = AC (hai cạnh tương ứng)
DB = DC (hai cạnh tương ứng)
Đúng 0
Bình luận (0)
cho tam giác ABC có góc A =90 độ; BC=2AB; E là trung điểm của BC. Tia phân giác của góc B cắt AC tại D.
a/chứng minh DB là tia phân giác của góc ADE
b/ chứng minh BD=DC
c/tính góc C, góc B của tam giác ABC
Cho tam giác ABC có góc B > C. Tia phân giác của góc A cắt BC ở D. Chứng minh rằng BD < DC
vì \(\widehat{B}>\widehat{C}\)nên AC > AB
Trên cạnh AC lấy điểm E sao cho AB = AE thì E nằm giữa A và C
\(\Delta ADB=\Delta ADE\)( c.g.c ) nên DB = DE và \(\widehat{DEC}=\widehat{CBx}\)
mà \(\widehat{DBx}>\widehat{C}\)nên \(\widehat{DEC}>\widehat{C}\), do đó : DC > DE
Vậy BD < DC
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc B > C. Tia phân giác của góc A cắt BC ở D. Chứng minh rằng BD < DC
Cho tam giác ABC có góc B > C. Tia phân giác của góc A cắt BC ở D. Chứng minh rằng BD < DC
Cho tam giác ABC có góc B > C. Tia phân giác của góc A cắt BC ở D. Chứng minh rằng BD < DC
Câu hỏi của nguyễn Như Quỳnh - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc B > C. Tia phân giác của góc A cắt BC ở D. Chứng minh rằng BD < DC
Cho tam giác ABC có góc B > góc C. Tia phân giác của góc A cắt BC ở D. Chứng minh rằng BD < DC.
Xét Tam giác ABC : Góc B lớn hơn góc C → AC > AB
Trên tia AC lấy điểm F sao cho AF =AB
Xét tam giác ADE và tam giác ADB có : AD chung
AF =AB ( cách vẽ )
Góc DAE = Góc DAB ( gt)
→ Tam giác ADE = Tam giác ADB (c.g.c) (1)
Từ (1) → Góc ADB = Góc ADE ( 2 góc tương ứng )
Lại có : Góc ADB là góc ngoài tại D của tam giác ADC → ADB > C
→ ADE > C
Mà : Góc DEC là góc ngoài tại E của tam giác ADE → DEC > ADE
→ DEC > C
Xét tam giác DEC có : DEC > C → DC > DE
Mặt khác từ (1) → DE =DB ( 2 cạnh tương ứng )
→ DC > DB
→ ĐPCM
Đúng 0
Bình luận (0)
mình viết nhầm E thành F bạn tự sửa nha
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có góc 30°,tia phân giác của góc B cắt AC tại D,kẻ DE vuông góc BC tại E. a)Chứng minh ∆ABD=∆AEBD b) Chứng minh tam giác ABE là tam giác đều c) Chứng minh BD=DC GIÚP TỚ VỚI Ạ !
a: XétΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó:ΔABD=ΔEBD
b: ta có: ΔABD=ΔEBD
nên BA=BE
=>ΔBAE cân tại B
mà \(\widehat{ABE}=60^0\)
nên ΔBAE đều
Đúng 0
Bình luận (0)












