Trong không gian Oxyz, cho bốn điểm A(-1;2;0), B(3;1;0), C(0;2;1), D(1;2;2). Trong đó có ba điểm thẳng hàng là
A. A, C, D
B. A, B, D
C. B, C, D
D. A, B, C
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A 1 ; - 2 ; 0 , B 1 ; 0 ; - 1 , C 0 ; - 1 ; 2 và D 0 ; m ; p . Hệ thức giữa m và p để bốn điểm A, B, C, D đồng phẳng là
A. 2 m + p = 0
B. m + p = 1
C. m + 2 p = 3
D. 2 m - 3 p = 0
Chọn đáp án C
Ta có A B ⇀ = 0 ; 2 ; - 1 , A C ⇀ = - 1 ; 1 ; 2 và A D ⇀ = - 1 ; m + 2 ; p .
Suy ra A B ⇀ , A C ⇀ = 5 ; 1 ; 2
⇒ A B ⇀ , A C ⇀ . A D ⇀ = m + 2 p - 3
Để bốn điểm A, B, C, D đồng phẳng thì A B ⇀ , A C ⇀ . A D ⇀
⇔ m + 2 p = 3
Trong không gian với hệ tọa độ Oxyz cho bốn điểm A 1 ; - 2 ; 0 , B 1 ; 0 ; - 1 , C 0 ; - 1 ; 2 và D 0 ; m ; p . Hệ thức giữa m và p để bốn điểm A, B, C, D đồng phẳng là
A. 2m + p = 0
B. m + p = 1
C. m + 2p = 3
D. 2m - 3p = 0
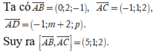
Để bốn điểm A, B, C, D đồng phẳng khi 
Chọn C.
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A - 1 ; 2 ; 1 , B - 4 ; 2 ; - 2 , C - 1 ; - 1 ; - 2 , D - 5 ; - 5 ; 2 . Tính khoảng cách từ điểm D đến mặt phẳng (ABC)
A. d = 3
B. d = 2 3
C. d = 3 3
D. d = 4 3
Chọn D.
Phương pháp : Sử dụng công thức tính thể tích ta có
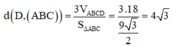
Trong không gian Oxyz, cho bốn điểm A(2;1;0), B(1;-1;3), C(3;-2;2) và D(-1;2;2). Hỏi có bao nhiêu mặt cầu tiếp xúc với tất cả bốn mặt phẳng (ABC), (BDC), (CDA), (DAB)?
A. 7.
B. 8.
C. vô số.
D. 6.
Trong không gian Oxyz, cho bốn điểm A 2 ; 0 ; 2 , B 1 ; - 1 ; - 2 , C - 1 ; 1 ; 0 , D - 2 ; 1 ; 2 .Thể tích của tứ diện ABCD bằng
A. 42 3
B. 14 3
C. 21 3
D. 7 3
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1;0;0),B(0;1;0),C(0;0;1),D(0;0;0). Hỏi có bao nhiêu điểm cách đều bốn mặt phẳng (ABC),(BCD),(CDA),(DBA)?
A. 5
B. 1
C. 8
D. 4
Phương trình mặt phẳng (ABC): x+y+z-1=0
Phương trình mặt phẳng (BCD): x=0
Phương trình mặt phẳng (CDA): y=0
Phương trình mặt phẳng (ĐBA): z=0
Gọi I(x;y;z) là điểm cách đều bốn mặt phẳng (ABC),(BCD),(CDA),(DBA)
⇒ x + y + z - 1 3 = x = y = z
TH1: x = y = z ⇒ 3 x - 1 3 = x
⇔ [ x = 1 3 + 3 x = 1 3 - 3 ⇒ I 1 3 + 3 ; 1 3 + 3 ; 1 3 + 3
hoặc I 1 3 - 3 ; 1 3 - 3 ; 1 3 - 3
TH2: - x = y = z ⇒ - x - 1 3 = x
⇔ [ x = 1 3 - 1 x = - 1 3 + 1 ⇒ I 1 3 - 1 ; - 1 3 - 1 ; - 1 3 - 1
hoặc I - 1 3 + 1 ; 1 3 + 1 ; 1 3 + 1
TH3: x = y = - z ⇒ x - 1 3 = x
hoặc I 1 3 - 1 ; - 1 3 - 1 ; 1 3 - 1
TH4: x = y = - z ⇒ x - 1 3 = x
⇔ [ x = - 1 3 - 1 x = 1 3 + 1 ⇒ I - 1 3 - 1 ; - 1 3 - 1 ; 1 3 - 1
hoặc I 1 3 + 1 ; 1 3 + 1 ; - 1 3 + 1
Vậy, có tất cả 8 điểm thỏa mãn.
Chọn đáp án C.
Trong không gian với hệ tọ độ Oxyz, cho bốn điểm A(1;0;0), B(0;1;0), C(0;0;1), D(0;0;0). Hỏi có bao nhiêu điểm cách đều bốn mặt phẳng (ABC), (BCD),(CDA), (DAB)?
A. 4
B. 5
C. 1
D. 8
Đáp án D
Gọi I(a;b;c) là điểm cách đều bốn mặt phẳng (ABC), (BCD),(CDA), (DAB)
Khi đó, ta có
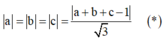
Suy ra có 8 cặp (a;b;c) thỏa mãn (*).
Trong không gian với hệ tọa độ, Oxyz cho bốn điểm A(0;0;6); B 0 ; 1 ; − 8 , C(1;2;-5) và D(4;3;8) Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó ?
A. Vô số
B. 1 mặt phẳng.
C. 7 mặt phẳng
D. 4 mặt phẳng.
Đáp án A.
Ta có A B ¯ = 0 ; 1 ; − 2 ; A C ¯ = 1 ; 2 ; 1 ⇒ A B ¯ ; A C ¯ = 5 ; − 2 ; − 1
Suy ra phương trình mặt phẳng (ABC) là 5 x − 2 y − z − 6 = 0.
Do đó, điểm thuộc mặt phẳng (ABC).
Vậy có vô số mặt phẳng cách đều bốn điểm đã cho.
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(0;0;-6), B(0;1;-8), C(1;2;-5), D(4;3;8). Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó?
A. Vô số
B. 1 mặt phẳng
C. 7 mặt phẳng
D. 4 mặt phẳng
Đáp án A
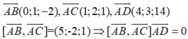
⇒ A B → , A C → , A D → đồng phẳng suy ra tồn tại vô số mặt phẳng cách đều 4 điểm trên
