Gọi c là đường thẳng đi qua điểm M (-1;4)và song song với đường thẳng y=x+2.Viết phương trình đường thẳng c.Giúp mình với ạ đang cần gấp
Những câu hỏi liên quan
cho đường tròn (O) đường kính AB. Đường thẳng a tiếp xúc với (O) tại A. Gọi M đi đông trên (O). Tiếp tuyến của (O) tại M cắt a tại C. Gọi I là tâm đường tròn tiếp xúc với a tại C đi qua M. Kẻ CD là đường kính (I). GỌi K là giao điểm của OC với (I). CMR
a, K là trung điểm của OC
b, ĐƯờng thẳng qua D vuông góc với BC luôn qua 1 điểm cố định
a) Ta có CA,CM là các tiếp tuyến từ C tới đường tròn (O) => OC là phân giác của ^AOM => ^MOC = ^AOC
Ta thấy ^CMD là góc chắn nửa đường tròn (I) => ^CMD = 900 => ^CMD + ^CMO = 1800
=> 3 điểm D,M,O thẳng hàng => ^DOC = ^MOC. Mà ^MOC = ^AOC nên ^DOC = ^AOC
Hai đường tròn (O),(I) cùng tiếp xúc với a => CD // AB (Cùng vuông góc với a)
Do đó ^AOC = ^DCO (So le trong) => ^DOC = ^DCO => \(\Delta\)ODC cân tại D
Lại có DK vuông góc OC tại K (Vì ^DKC chắn nửa đường tròn) => K là trung điểm OC (đpcm).
b) Gọi đường thẳng qua D vuông góc với BC cắt BC,AB lần lượt tại H,S.
Dễ thấy điểm H nằm trên đường tròn (I) => ^HMO = ^HCD = ^HBO (Do CD // AB)
=> Tứ giác HOBM nội tiếp => ^OHB = ^OMB => 900 - ^OHB = 900 - ^OMB
=> ^OHS = 900 - ^ABM = ^MAB = ^ACO (Cùng phụ ^CAM) (1)
Ta lại có ^SHK = ^DCK = ^SOK (Vì AB // CD) => Tứ giác KHOS nội tiếp => ^OHS = ^OKS (2)
Từ (1) và (2) suy ra ^ACO = ^OKS => KS // AC. Xét \(\Delta\)CAO có:
K là trung điểm cạnh OC (cmt), KS // AC (cmt), S thuộc OA => S là trung điểm cạnh OA
Do 2 điểm O,A cố định nên S cũng cố định. Mà đường thẳng qua D vuông góc BC cắt OA tại S
Nên ta có ĐPCM.
Đúng 0
Bình luận (0)
vẽ theo mô tả
cho 3 điểm ABC ko thẳng hàng
vẽ đường thẳng m đi qua 2 điểm A,B
vẽ đường thẳng n đi qua 2 điểm A,C
vẽ điểm D sao cho điểm C nằm giữa hai điểm A và điểm D
qua C , vẽ đường thẳng p song song với đường thẳng AB
gọi E là giao điểm của đường thẳng p và đường thẳng đi qua hai điểm D,B
Cho tam giác ABC cân tại A. Đường thẳng đi qua B song song với AC cắt đường thẳng đi qua C song song với AB tại D.a) (1 điểm). Chứng minh tứ giác ABDC là hình thoi;b) (0,75 điểm). Gọi M là điểm đối xứng với A qua C. Chứng minh AD vuông góc với DM;c) (0,75 điểm). Gọi E là giao điểm của AD và BC, O là giao điểm của CD và BM, F là giao của tia EO và DM. Chứng minh DF FM;d) (0,5 điểm). Gọi G là giao điểm của EM và CD. Chứng minh A, G, F thẳng hàng.
Đọc tiếp
Cho tam giác ABC cân tại A. Đường thẳng đi qua B song song với AC cắt đường thẳng đi qua C song song với AB tại D.
a) (1 điểm). Chứng minh tứ giác ABDC là hình thoi;
b) (0,75 điểm). Gọi M là điểm đối xứng với A qua C. Chứng minh AD vuông góc với DM;
c) (0,75 điểm). Gọi E là giao điểm của AD và BC, O là giao điểm của CD và BM, F là giao của tia EO và DM. Chứng minh DF = FM;
d) (0,5 điểm). Gọi G là giao điểm của EM và CD. Chứng minh A, G, F thẳng hàng.
1/ Cho 42 đường thẳng và điểm M.
Gọi x là số đường thẳng đi qua điểm M. Gọi y là số đường thẳng không đi qua điểm M.
Tìm x,y biết rằng x=5.y
2/ Với 2016, điểm thẳng hàng. Hỏi bao nhiêu điểm nằm giữa 2 điểm khác?
AI BIẾT THÌ GIÚP MÌNH VỚI NHÉ!!!
Trong Hình 5 có ba đoạn thẳng được đánh số (1), (2), (3) và hai điểm M, N
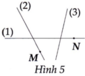
Hãy xác định đường thẳng nào là đường
thẳng a, b ,c biết
- Đường thẳng a đi qua điểm M;
- Đường thẳng b chứa điểm N;
- Đường thẳng c không đi qua điểm M và cũng không đi qua điểm N
Đường thẳng a là đường thăng số (2). Đường thẳng b là đường thẳng số (1). Đường thẳng c là đường thẳng số (3).
Đúng 1
Bình luận (0)
ngu hahahahahahahahahahahahahahahahahahahahahahaha
Trong Hình 5 có ba đoạn thẳng đượcĐánh số (1), (2), (3) và hai điểm M, NHãy xác định đường thẳng nào là đườngthẳng a, b ,c biết- Đường thẳng a đi qua điểm M;- Đường thẳng b chứa điểm N;- Đường thẳng c không đi qua điểm M và cũng không đi qua điểm N
Đọc tiếp
Trong Hình 5 có ba đoạn thẳng được
Đánh số (1), (2), (3) và hai điểm M, N
Hãy xác định đường thẳng nào là đường
thẳng a, b ,c biết
- Đường thẳng a đi qua điểm M;
- Đường thẳng b chứa điểm N;
- Đường thẳng c không đi qua điểm M và cũng không đi qua điểm N
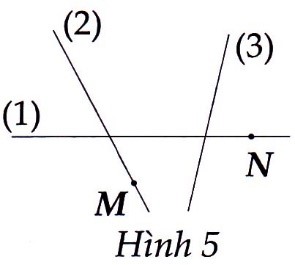
Đường thẳng a là đường thăng số (2). Đường thẳng b là đường thẳng số (1). Đường thẳng c là đường thẳng số (3).
Đúng 0
Bình luận (0)
NGU hahahahahahahahahahahahahahahahahaha
Gọi (C) là đồ thị hàm số
y
x
2
+
2
x
+
1
, M là điểm di chuyển trên
C
;
M
t
,
M
z
là các đường thẳng đi qua M sao cho Mt song song với trục tung đồng thời tiếp tuyến của (C) tại M là phân giác của góc tạo bởi hai đường thẳng
M
t
,
M
z
.
Khi M di chuyển...
Đọc tiếp
Gọi (C) là đồ thị hàm số y = x 2 + 2 x + 1 , M là điểm di chuyển trên C ; M t , M z là các đường thẳng đi qua M sao cho Mt song song với trục tung đồng thời tiếp tuyến của (C) tại M là phân giác của góc tạo bởi hai đường thẳng M t , M z . Khi M di chuyển trên (C) thì Mz luôn đi qua điểm cố định nào dưới đây?
A. M 0 − 1 ; 1 4
B. M 0 − 1 ; 1 2
C. M 0 − 1 ; 1
D. M 0 − 1 ; 0
Đáp án D
Gọi M a ; a 2 + 2 a + 1 ⇒ M t : x = a
Lại có y ' = 2 x + 2 do đó PTTT tại M là: y = 2 a + 2 x − a + a 2 + 2 a + 1
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O có đường kính AB. Lấy điểm C trên đoạn AO. Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn tại K. Gọi M là điểm bất kì trên cung KB. Đường thẳng CK cắt các đường thẳng AM, BM lần lượt tại H, D. Đường thẳng BH cắt nửa đường tròn tại Na. CM: ACMD nội tiếpb. CA.CBCH.CDc. CM: A,N,D thẳng hàng và tiếp tuyến N đi qua trung điểm DHd. Khi M di động trên cung KB, c/m đt MN luôn đi qua 1 điểm cố định.
Đọc tiếp
Cho nửa đường tròn tâm O có đường kính AB. Lấy điểm C trên đoạn AO. Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn tại K. Gọi M là điểm bất kì trên cung KB. Đường thẳng CK cắt các đường thẳng AM, BM lần lượt tại H, D. Đường thẳng BH cắt nửa đường tròn tại N
a. CM: ACMD nội tiếp
b. CA.CB=CH.CD
c. CM: A,N,D thẳng hàng và tiếp tuyến N đi qua trung điểm DH
d. Khi M di động trên cung KB, c/m đt MN luôn đi qua 1 điểm cố định.
câu này là đề hình của 1 năm nào đó mà trong quyển ôn thi vào 10 môn toán có bn nhé! cũng không khó lắm đâu lời giải rất chi tiết hình như là đề 3 đấy (phàn đề thật)
Đúng 0
Bình luận (0)
Cho điểm M(2;1;0) và đường thẳng
∆
:
x
-
1
2
y
+
1
1
z
-
1
Gọi d là đường thẳng đi qua M, cắt và vuông góc với
∆
. Đường thẳng d có một VTCP là
Đọc tiếp
Cho điểm M(2;1;0) và đường thẳng ∆ : x - 1 2 = y + 1 1 = z - 1 Gọi d là đường thẳng đi qua M, cắt và vuông góc với ∆ . Đường thẳng d có một VTCP là
Cho điểm M(2;1;0) và đường thẳng
Δ
:
x
-
1
2
y
+
1
1
z
-
1
.
Gọi d là đường thẳng đi qua M, cắt và vuông góc với
∆
. Đường thẳng d có một VTCP là A.
u
→...
Đọc tiếp
Cho điểm M(2;1;0) và đường thẳng Δ : x - 1 2 = y + 1 1 = z - 1 . Gọi d là đường thẳng đi qua M, cắt và vuông góc với ∆ . Đường thẳng d có một VTCP là
A. u → = ( - 3 ; 0 ; 2 )
B. u → = ( 0 ; 3 ; 1 )
C. u → = ( 0 ; 3 ; 1 )
D. u → = ( 1 ; - 4 ; - 2 )
