Hàm số y = f(x) liên tục và có bảng biến thiên trong đoạn [-1;3] cho trong hình bên. Gọi M là giá trị lớn nhất của hàm số y= f(x) trên đoạn [-1;3]. Tìm mệnh đề đúng?
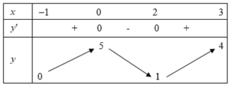
A. ![]()
B. ![]()
C. ![]()
D. ![]() .
.
Hàm số y=f(x) liên tục và có bảng biến thiên trong đoạn [-1;3] cho trong hình bên. Gọi M là giá trị lớn nhất của hàm số y=f(x) trên đoạn [-1;3]. Tìm mệnh đề đúng?
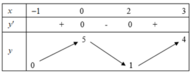
A. M=f(-1).
B. M=f(3).
C. M=f(2).
D. M=f(0).
Cho hàm số y=f(x) xác định và liên tục trên tập D = ℝ \ { - 1 } và có bảng biến thiên:
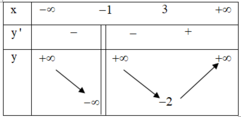
Dựa vào bảng biến thiên của hàm số y=f(x) Khẳng định nào sau đây là khẳng
định sai?
A. Giá trị nhỏ nhất của hàm số trên đoạn [ 1 ; 8 ] bằng -2
B. Phương trình f(x)=m có 3 nghiệm thực phân biệt khi x > -2
C. Hàm số đạt cực tiểu tại x=3
D. Hàm số nghịch biến trên khoảng ( - ∞ ; 3 )
Đáp án D
Tại -1 hàm số không xác định nên không nghịch biến trên ( - ∞ ; 3 )
Cho hàm số y = f ( x ) xác định và liên tục trên tập D = ℝ \ 1 và có bảng biến thiên
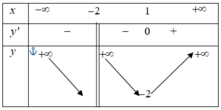
Dựa vào bảng biến thiên của hàm số y = f x . Khẳng định nào sau đây là sai?
A. Phương trình f x = m có 3 nghiệm thực phân biệt khi x > -2
B. Giá trị nhỏ nhất của hàm số trên đoạn 0 ; 6 là -2
C. Hàm số đạt cực tiểu tại x = 1
D. Hàm số nghịch biến trên khoảng − ∞ ; 1
Đáp án D
Khẳng định sai là “Hàm số nghịch biến trên khoảng − ∞ ; 1 ” do hàm số không xác định tại x = - 2
Cho hàm số y=f(x) liên tục và có bảng biến thiên như sau
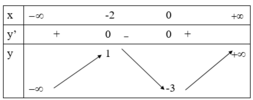
Hàm số y= f(x) nghịch biến trên khoảng nào dưới đây?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = f(x) liên tục và có bảng biến thiên như sau:
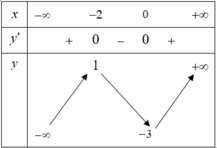
Hàm số y=f(x) nghịch biến trên khoảng nào dưới đây?
![]()
![]()
![]()
![]()
Cho hàm số y = f(x) có đạo hàm f'(x). Hàm số y = f'(x) liên tục trên tập số thực và có bảng biến thiên như sau:
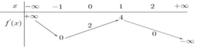
Biết rằng f(-1) = 10 3 , f(2) = 6. Giá trị nhỏ nhất của hàm số g(x) = f 3 ( x ) - 3 f ( x ) trên đoạn [-1;2] bằng
A. 10 3
B. 820 27
C. 730 27
D. 198
Chọn C
Xét hàm số g(x) = f 3 ( x ) - 3 f ( x ) trên đoạn [-1;2]
![]()
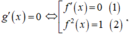
Từ bảng biến thiên, ta có:
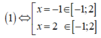
Và ![]() nên f(x) đồng biến trên [-1;2]
nên f(x) đồng biến trên [-1;2]
![]()
![]() nên (2) vô nghiệm
nên (2) vô nghiệm
Do đó, g'(x) = 0 chỉ có nghiệm là x = -1 và x = 2
Ta có ![]()
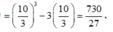
![]()
Vậy ![]()
Cho hàm số f(x) liên tục trên đoạn [-3;5] và có bảng biến thiên như hình vẽ
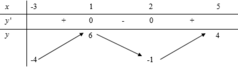
A. 2
B. 5
C. 3
D. 0.
Cho hàm số y = f(x) xác định, liên tục trên [-1; 1] và có bảng biến thiên như sau: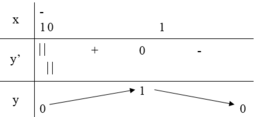
![]()
![]()
![]()
![]()
Cho hàm số f(x) có đạo hàm liên tục trên ℝ . Bảng biến thiên của hàm số f’(x) trên đoạn [-1;3] như hình
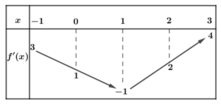
Hàm số g x = f 1 - x 2 + x nghịch biến trên khoảng nào trong các khoảng sau ?
A. (-4;-2)
B. (-2;0)
C. (0;2)
D. (2;4)
Ta có ![]()
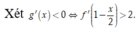
= TH1: ![]() Do đó hàm số nghịch biến trên (-4;-2)
Do đó hàm số nghịch biến trên (-4;-2)
= TH2: ![]() nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
nên hàm số chỉ nghịch biến trên khoảng (2-2a;4) chứ không nghịch biến trên toàn khoảng (2;4)
Vậy hàm số 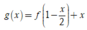 nghịch biến trên (-4;-2)
nghịch biến trên (-4;-2)
Chọn A.