Tìm giá trị nhỏ nhất của hàm số sau trên đoạn [1;3] : \(f\left(x\right)=3x^2+\frac{8}{x}\)
( Sử dụng BĐT Cauchy)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = 1/sinx trên đoạn [ π /3; 5 π /6]
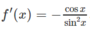
f′(x) < 0 nên và f’(x) > 0 trên ( π /2; 5 π /6] nên hàm số đạt cực tiểu tại x = π /2 và f CT = f( π /2) = 1
Mặt khác, f( π /3) = 2 3 , f(5 π /6) = 2
Vậy min f(x) = 1; max f(x) = 2
\(f\left(x\right)=e^{sinx}-sinx-1\)
\(\Rightarrow f'\left(x\right)=cosx.e^{sinx}-cosx=cosx\left(e^{sinx}-1\right)\)
\(f'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sinx=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{\pi}{2}\\x=\pi\end{matrix}\right.\)
\(f\left(0\right)=0\) ; \(f\left(\dfrac{\pi}{2}\right)=e-2\) ; \(f\left(\pi\right)=0\)
\(\Rightarrow f\left(x\right)_{min}=0\) ; \(f\left(x\right)_{max}=e-2\)
Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau trên các khoảng, đoạn tương ứng: f(x) = x 4 – 4 x 2 + 1 trên đoạn [-1; 2]
min f(x) = f( 2 ) = −3; max f(x) = f(2) = f(0) = 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 2 x trên đoạn [-1; 1].
Trên đoạn [-1; 1], ta có :
y = log 5 x
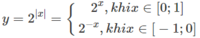
Do đó, trên đoạn [0;1] hàm số đồng biến, trên đoạn [-1;0] hàm số nghịch biến. Suy ra các giá trị lớn nhất và giá trị nhỏ nhất sẽ đạt được tại các đầu mút.
Ta có: y(−1) = 2 - - 1 = 2 1 = 2, y(0) = 2 0 = 1, y(1) = 2 1 = 2
Vậy max y = y(1) = y(−1) = 2, min y = y(0) = 1.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 2 x trên đoạn [-1; 1].
Trên đoạn [-1; 1], ta có :
y = log 5 x
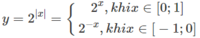
Do đó, trên đoạn [0;1] hàm số đồng biến, trên đoạn [-1;0] hàm số nghịch biến. Suy ra các giá trị lớn nhất và giá trị nhỏ nhất sẽ đạt được tại các đầu mút.
Ta có: y(−1) = 2 - ( - 1 ) = 2 1 = 2, y(0) = 2 0 = 1, y(1) = 2 1 = 2
Vậy max y = y(1) = y(−1) = 2, min y = y(0) = 1.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = 25 - x 2 trên đoạn [-4; 4]
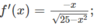
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f CĐ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 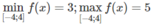
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:
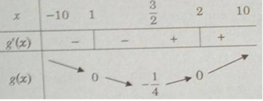
Vì
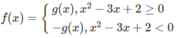
nên ta có đồ thị f(x) như sau:
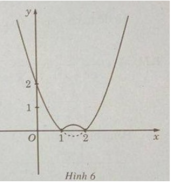
Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau trên đoạn [2;4]
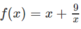
(Đề thi tốt nghiệp THPT năm 2008)
TXĐ: D = R\{0}
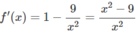
f′(x) = 0 ⇔ x = 3 hoặc x = -3
Hàm số nghịch biến trong các khoảng (-3;0), (0;3) và đồng biến trong các khoảng (− ∞ ;3), (3;+ ∞ )
Bảng biến thiên:
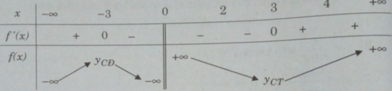
Ta có: [2;4] ⊂ (0; + ∞ ); f(2) = 6,5; f(3) = 6; f(4) = 6,25
Suy ra
min f(x) = f(3) = 6; max f(x) = f(2) = 6,5
TXĐ: D = R\{0}
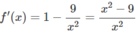
f′(x) = 0 ⇔ x = 3 hoặc x = -3
Hàm số nghịch biến trong các khoảng (-3;0), (0;3) và đồng biến trong các khoảng (− ∞ ;3), (3;+ ∞ )
Bảng biến thiên:

Ta có: [2;4] ⊂ (0; + ∞ ); f(2) = 6,5; f(3) = 6; f(4) = 6,25
Suy ra
min f(x) = f(3) = 6; max f(x) = f(2) = 6,5
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 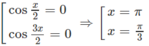
Ta có: f(0) = 0,
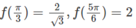
Từ đó ta có: min f(x) = −2 ; max f(x) = 3 3 /2
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 3 e - 2 x trên đoạn [-1; 4]
A. m a x 1 ; 4 y = 27 e 2 8 , m i n 1 ; 4 y = 64 e - 8
B. m a x 1 ; 4 y = 27 e = 3 8 , m i n 1 ; 4 y = e - 2
C. m a x 1 ; 4 y = e - 2 , m i n 1 ; 4 y = 64 e - 8
D. m a x 1 ; 4 y = 27 e 2 8 , m i n 1 ; 4 y = 0