Tìm số giá trị nguyên thuộc đoạn [-2019;2019] của tham số m để đồ thị hàm số y = x - 3 x 2 + x - m có đúng hai đường tiệm cận.
A. 2007
B. 2010
C. 2009
D. 2008
Số giá trị nguyên m thuộc đoạn [-2019; 2019] để phương trình
4 x - ( m - 3 ) . 2 x + 3 m + 1 = 0
có đúng một nghiệm lớn hơn 0 là:
A. 2021
B. 2022
C. 2019
D. 2020
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn - 10 ; 10 để hàm số y = x 3 - 3 x 2 + 3 m x + 2019 nghịch biến trên khoảng 1 ; 2 ?
A. 11
B. 20
C. 10
D. 21
Chọn A.
TXĐ: D = R
Ta có: y ' = 3 x 2 - 6 x + 3 m
Để hàm số đã cho nghịch biến trên 1 ; 2
thì y ' ≤ 0 , ∀ x ∈ 1 ; 2 và bằng 0 tại hữu hạn điểm
![]()
![]()
![]()
![]()
Hàm số y = x - 1 2 đồng biến trên 1 ; + ∞ nên cũng đồng biến trên 1 ; 2
![]()
![]()
Lại có m ∈ - 10 ; 10 và m ∈ Z nên m ∈ - 10 ; - 9 ; . . ; 0
Vậy có 11 giá trị của m
Cho hàm số y = 2 m 3 - 1 4 - 2 x 3 + 2 m - 7 x 2 - 12 x + 2019 . Có bao nhiêu giá trị nguyên của m thuộc đoạn - 15 ; 15 để hàm số đã cho đồng biến trên đoạn - 1 2 ; - 1 4
A. 15
B. 13
C. 28
D. 23
Có bao nhiêu giá trị nguyên thuộc đoạn [0;2019] của tham số m để phương trình 4 x - m + 2018 2 x + 2019 + 3 m = 0 có hai nghiệm trái dấu?
A.2016
B.2019
C.2013
D.2018
Tìm tất cả các giá trị nguyên thuộc [-2019; 2019]của tham
số m để phương trình \(x^4-2mx^3+x^2-2mx+1=0\) có nghiệm.
A. 2019 . B. 3039 . C. 4038 . D. 4041.
Cho hàm số f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên. Số giá trị nguyên của tham số m để phương trình f 2 cos x + m - 2018 f cos x + m - 2019 = 0 có đúng 6 nghiệm phân biệt thuộc đoạn 0 ; 2 π là
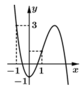
A. 1
B. 2
C. 3
D. 5
Có ![]()
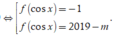
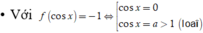
![]()
Phương trình này có hai nghiệm ![]()
• Với ![]() ta cần tìm điều kiện để phương trình này có 4 nghiệm phân biệt thuộc
ta cần tìm điều kiện để phương trình này có 4 nghiệm phân biệt thuộc ![]()
![]()
![]()
Với t = -1 phương trình (1) cho đúng một nghiệm x =
π
; với t = 0 phương trình cho hai nghiệm ![]()
Với mỗi ![]() phương trình cho hai nghiệm thuộc
phương trình cho hai nghiệm thuộc![]()
Vậy điều kiện cần tìm là phương trình (1) phải có hai nghiệm phân biệt
![]()
![]()
Chọn B.
Có bao nhiêu giá trị nguyên của a thuộc khoảng (-2019; 2019) để l i m ( 4 n 2 + 3 n - 2 + a n - 3 ) = + ∞ ?
A. 2018
B. 2019
C. 2020
D. 2021
Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng (0; 2019) để l i m 9 n + 3 n + 1 5 n + 9 n + a ≤ 1 2187 ?
A. 2011
B. 2018
C. 2019
D. 2012
Có bao nhiêu giá trị nguyên của m thuộc khoảng (-2019; 2019) để hàm số sau có tập xác định là D = R
y = x + m + x 2 + 2 ( m + 1 ) x + m 2 + 2 m + 4 + log 2 ( x - m + 2 x 2 + 1 )
A. 2020
B. 2021
C. 2018
D. 2019
Tìm số giá trị nguyên của m để phương trình log 3 2 log 3 2 x + 1 - 2 m - 1 = 0 có ít nhất một nghiệm thuộc đoạn 1 ; 3 3
A. 1
B. 2
C. 3
D. 4
Đặt t = log 3 2 x + 1 . Do 1 ≤ x ≤ 3 3 nên 1 ≤ t ≤ 2
Phương trình đã cho có ít nhất một nghiệm thuộc đoạn 1 ; 3 3
⇔ Phương trình t 2 - 1 + t - 2 m - 1 = 0 có ít nhất một nghiệm thuộc đoạn [ 1;2 ]
⇔ Phương trình t 2 + t - 2 = 2 m có ít nhất một nghiệm thuộc đoạn [ 1;2 ]
Xét hàm số f t = t 2 + t - 2 , t ∈ 1 ; 2
f ' t = 2 t + 1 > 0 , ∀ t ∈ 1 ; 2 ⇒ là hàm đồng biến trên [ 1;2 ] ⇒ f 1 ≤ f t ≤ f 2 ⇔ 0 ≤ m ≤ 2
Vậy có 3 giá trị nguyên của m thỏa mãn yêu cầu bài toán
Đáp án C