Cho hàm số f(x) có nguyên hàm là F(x) trên đoạn [1;2], biết F(2) = 1 và ∫ 1 2 F ( x ) d x = 5 . Tính I= ∫ 1 2 ( x - 1 ) f ( x ) d x
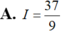
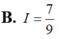
![]()
![]()
Cho hàm số f(x) có nguyên hàm là F(x) trên đoạn [1;2], biết F(2)=1 và ∫ 1 2 F ( x ) d x = 5 . Tính I = ∫ 1 2 ( x - 1 ) f ( x ) d x
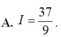
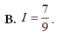
![]()
![]()
Cho hàm số y = f ( x ) liên tục trên R và có đạo hàm f ' ( x ) = x 2 ( x - 2 ) ( x 2 - 6 x + m ) , với mọi x ∈ R . Có bao nhiêu số nguyên m thuộc đoạn - 2019 ; 2019 để hàm số g ( x ) = f ( 1 - x ) nghịch biến trên khoảng - ∞ ; - 1
A. 2012
B. 2011
C. 2009
D. 2010
Cho hàm số y=f(x) liên tục trên R và có đạo hàm f ' x = x 2 x - 2 x 2 - 6 x + m với mọi x ∈ ℝ Có bao nhiêu số nguyên m thuộc đoạn [-2019;2019] để hàm số g(x)=f(1-x) nghịch biến trên khoảng - ∞ ; - 1
A. 2010
B. 2012
C. 2011
D. 2009
Cho F(x) là một nguyên hàm của hàm số f(x) trên đoạn [1;3], F(1)=3,F(3)=5 và ∫ 1 3 ( x 4 - 8 x ) f ( x ) dx = 12 . Tính I = ∫ 1 3 ( x 3 - 2 ) F ( x ) dx .
A. I= 147 2
B. I= 147 3
C. I= - 147 2
D. I= 147.
Cho hàm số f(x) có đạo hàmf'(x) xác định và liên tục trên đoạn [0;6]. Đồ thị hàm số y=f'(x) như hình vẽ bên. Biết f(0)=f(3)=f(6)=-1,f(1)=f(5)=1. Số điểm cực trị của hàm số y = [ f ( x ) ] 2 trên đoạn [0;6] là
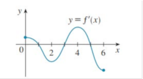
A. 5.
B. 7.
C. 9.
D. 8.
Cho hàm số y = f(x) xác định trên tập số thực và có đạo hàm f'(x). Đồ thị hàm số y = f'(x) được cho bởi hình bên dưới. Biết rằng f(0) + f(1) - 2f(2) = f(4). - f(3). Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [0;4] là
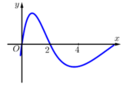
A. f(1)
B. f(0)
C. f(2)
D. f(4)
Chọn D
Từ đồ thị của hàm số y = f'(x) ta suy ra bảng biến thiên của hàm số y = f(x) trên đoạn như sau:
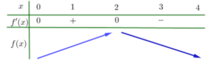
Từ bảng biến thiên, ta có nhận xét sau: ![]()
![]()
Ta lại có: f(0) + f(1) - 2f(2) = f(4). - f(3)
![]()
![]()
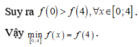
Cho hàm số f(x) có đạo hàm là f'(x). Đồ thị của hàm số y = f'(x) được cho như hình vẽ dưới đây:
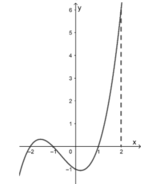
Biết rằng f(-1) + f(0) < f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x) trên đoạn [-1;2] lần lượt là:
A. f(1);f(2)
B. f(2);f(0)
C. f(0);f(2)
D. f(1);f(-1)
Chọn A
Từ đồ thị của hàm số y = f'(x) ta có bảng biến thiên của hàm số y = f(x) trên đoạn [-1;2] như sau
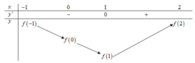
Nhận thấy
![]()
Để tìm ![]() ta so sánh f(-1) và f(2)
ta so sánh f(-1) và f(2)
Theo giả thiết, ![]()
![]()
Từ bảng biến thiên , ta có f(0) - f(1) > 0. Do đó f(2) - f(-1) > 0 ![]()
![]()
Biết F(x) là một số nguyên hàm của hàm số f(x) trên đoạn [-1;0], F - 1 = - 1 ; F 0 = 0 và ∫ - 1 0 2 3 x F ( x ) dx = - 1 . Tính I= ∫ - 1 0 2 3 x f ( x ) dx .
A. 1 8 - 3 ln 2
B. 1 8 + ln 2
C. 1 8 + 3 ln 2
D. - 1 8 + 3 ln 2
Cho hàm số y = f(x) có đạo hàm f'(x) = x(x+1) x - 2 2 với mọi x ∈ ℝ . Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [-1;2] là
A. f(-1)
B. f(0)
C. f(3)
D. f(2)