Trong không gian Oxyz, gọi d là đường thẳng đi qua điểm A(1;-1;2), song song với mặt phẳng (P): 2x-y-z+3=0, đồng thời tạo với đường thẳng △ : x + 1 1 = y - 1 - 2 = z 2 một góc lớn nhất. Phương trình đường thẳng d là
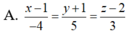
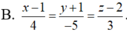
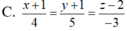
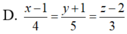
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ : x + 1 2 = y 3 = z + 1 - 1 và hai điểm A(1; 2; -1); B (3; -1; -5). Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ điểm B đến đường thẳng d là lớn nhất. Phương trình đường thẳng d là:
A . x - 3 2 = y 2 = z + 5 - 1
B . x - 1 = y + 2 3 = z 4
C . x + 2 3 = y 1 = z - 1 - 1
D. Tất cả sai
Chọn D
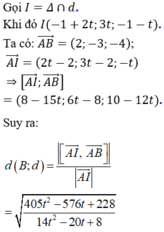
Xét hàm số:
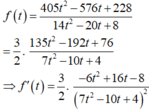
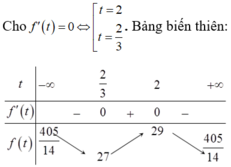
Do đó d (B; d) nhỏ nhất khi f(t) đạt giá trị nhỏ nhất bằng 27 tại t = 2/3. Suy ra ![]() . Chọn một vectơ chỉ phương của đường thẳng d là
. Chọn một vectơ chỉ phương của đường thẳng d là ![]()
Vậy phương trình đường thẳng ![]()
Trong không gian Oxyz, cho đường thẳng d : x - 1 1 = y - 1 - 2 = z - 1 2 Gọi ∆ là đường thẳng đi qua điểm A(1;1;1) và có véc tơ chỉ phương u ⇀ ( 3 ; 4 ; 0 ) Đường phân giác góc tù tạo bởi d và ∆ có phương trình là
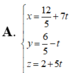
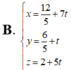
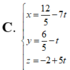
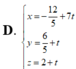
Trong không gian Oxyz, gọi d là đường thẳng đi qua điểm A(1;-1;2), song song với mặt phẳng (P): 2x-y-z+3=0, đồng thời tạo với đường thẳng ∆ : x + 1 1 = y - 1 - 2 = z 2 một góc lớn nhất. Phương trình đường thẳng d là.
![]()
![]()
![]()
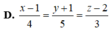
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ : x + 1 2 = y 3 = z + 1 − 1 và hai điểm A 1 ; 2 ; − 1 , B 3 ; − 1 ; − 5 . Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ B đến đường thẳng d là lớn nhất. Khi đó, gọi M a ; b ; c là giao điểm của d với đường thẳng Δ . Giá trị P = a + b + c bằng
A. -2
B. 4
C. 2
D. 6

- Tính khoảng cách từ B đến d theo t và tìm GTLN của khoảng cách.
- Tìm t và suy ra tọa độ của M.
Cách giải:
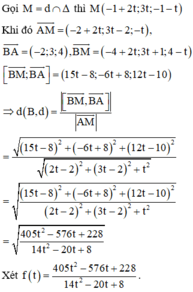
Sử dụng MTCT (chức năng TABLE với bước START nhập -5, bước END nhập 5 và bước STEP nhập 1 ta sẽ được kết quả GTLN f t = 29 tại t = 2)

Trong không gian Oxyz cho bốn điểm A(3;0;0),B(0;2;0),C(0;0;6) và D(1;1;1) Gọi ∆ là đường thẳng đi qua D và thỏa mãn tổng khoảng cách từ các điểm A,B,C đến ∆ là lớn nhất, hỏi ∆ đi qua điểm nào trong các điểm dưới đây?
A. M(5;7;3)
B. M(3;4;3)
C. M(7;13;5)
D. M(-1;-2;1)
Phương trình mặt phẳng (ABC) là x 3 + y 2 + z 6 = 1 →2x+3y+z-6=0
Dễ thấy D ϵ (ABC). Gọi H,K,I lần lượt là hình chiếu của A,B,C trên ∆.
Do ∆ là đường thẳng đi qua D nên AH≤ AD,BK≤ BD,CI≤ CD.
Vậy để khoảng cách từ các điểm A,B,C đến ∆ là lớn nhất thì ∆ là đường thẳng đi qua D và vuông góc với (ABC). Vậy phương trình đường thẳng ∆ là x = 1 + 2 t y = 1 + 3 t ( t ∈ ℝ ) z = 1 + t . Kiểm tra ta thấy điểm M(5;7;3) ϵ ∆
Đáp án A
Trong không gian Oxyz cho bốn điểm A(3;0;0), B(0;2;0), C(0;0;6), D(1;1;1) Gọi △ là đường thẳng đi qua D và thỏa mãn tổng khoảng cách từ các điểm A,B,C đến △ là lớn nhất, hỏi △ đi qua điểm nào trong các điểm dưới đây?
A. M(-1;-2;1)
B. (5;7;3)
C. M(3;4;3)
D. M(7;13;5)
Trong không gian với hệ tọa độ Oxyz, gọi d đi qua điểm A ( 1;-1;2 ) , song song với (P): 2x - y - z + 3 = 0, đồng thời tạo với đường thẳng ∆ : x + 1 1 = y - 1 - 2 = z 2 một góc lớn nhất. Phương trình đường thẳng d là.
A. x - 1 1 = y + 1 - 5 = z - 2 7
B. x - 1 4 = y + 1 - 5 = z + 2 7
C. x - 1 4 = y + 1 5 = z - 2 7
D. x - 1 1 = y + 1 - 5 = z - 2 - 7
Đường thẳng d đi qua A ( 1;-1;2 ) có vec tơ chỉ phương u → ( a ; b ; c ) do d song song (P): 2x - y - z + 3 = 0 nên u → ( a ; b ; c ) ⊥ n ( 2;-1;1 )
⇔ u → . n = 0 ⇔ 2a = b + c
Đến đây ta kiểm tra chỉ có đáp án A là đường thẳng có véc tơ chỉ phương thỏa mãn (1) nên ta chọn đáp án A
Đáp án cần chọn là A
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(2;0;0), B(0;3;0), C0;0;6) và D(1;1;1). Gọi ∆ là đường thẳng đi qua D và thỏa mãn tổng khoảng cách từ các điểm A, B, C đến ∆ là lớn nhất. Khi đó ∆ đi qua điểm nào trong các điểm dưới đây?
A. M(-1;-2;1)
B. M(5;7;3)
C. M(4;3;7)
D. M(3;4;3)
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;0;-1) và đường thẳng d x = t y = - 1 + 2 t z = - t . Gọi (P) là mặt phẳng chứa đường thẳng dvà đi qua A. Viết phương trình mặt cầu tâm O tiếp xúc với mặt phẳng(P).
A. ( S ) : x 2 + y 2 + z 2 = 1 3
B. ( S ) : x 2 + y 2 + z 2 = 1 3
C. ( S ) : x 2 + y 2 + z 2 = 3
D. ( S ) : x 2 + y 2 + z 2 = 3