Trong không gian Oxyz, cho (S) là tập hợp các điểm M(x; y; z) có tọa độ thỏa mãn phương trình
(S): x2 + y2 + z2 – 4x + 6y – 12 = 0.
Chứng minh rằng (S) là một mặt cầu. Xác định tâm và tính bán kính của mặt cầu đó.
Những câu hỏi liên quan
Trong không gian Oxyz, cho A(1;0;-3), B(-3;-2;-5). Biết rằng tập hợp các điểm M trong không gian tỏa mãn đẳng thức
AM
2
+
2
BM
2
30 là một mặt cầu (S). Tìm tọa độ tâm I và bán kính R của (S). A. I(-1; -1; -4); R
9
B. I(-2; -2; -8); R 3 C. I(-1; -1; -4); R
30
/2 D. I(-1; -1; -4); R 3
Đọc tiếp
Trong không gian Oxyz, cho A(1;0;-3), B(-3;-2;-5). Biết rằng tập hợp các điểm M trong không gian tỏa mãn đẳng thức AM 2 + 2 BM 2 = 30 là một mặt cầu (S). Tìm tọa độ tâm I và bán kính R của (S).
A. I(-1; -1; -4); R = 9
B. I(-2; -2; -8); R = 3
C. I(-1; -1; -4); R = 30 /2
D. I(-1; -1; -4); R = 3
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm
A
1
;
0
;
−
3
,
B
−
3
;
−
2
;
−
5
.
Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức
A...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A 1 ; 0 ; − 3 , B − 3 ; − 2 ; − 5 . Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức A M 2 + B M 2 = 30 là một mặt cầu (S), tọa độ tâm I và bán kính R của mặt cầu (S) là
A. I − 2 ; − 2 ; − 8 , R = 3
B. I − 1 ; − 1 ; − 4 , R = 6
C. I − 1 ; − 1 ; − 4 , R = 3
D. I − 1 ; − 1 ; − 4 , R = 30 2
Đáp án C
Gọi M x ; y ; z ⇒ A M → = x − 1 ; y ; z + 3 , B M → = x + 3 ; y + 2 ; z + 5
Khi đó A M 2 + B M 2 = 30 ⇔ x − 1 2 + y 2 + z + 3 2 + x + 3 2 + y + 2 2 + z + 5 2 = 30
⇔ x − 1 2 + y + 1 2 + z + 4 2 = 9 ⇒ M ∈ S có tâm I − 1 ; − 1 ; − 4 , R = 3
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm
A
1
;
0
;
-
3
,
-
3
;
-
2
;
-
5
. Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức
A
M...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A 1 ; 0 ; - 3 , - 3 ; - 2 ; - 5 . Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức A M 2 + B M 2 = 30 là một mặt cầu (S). Tọa độ tâm I và bán kinh R của mặt cầu (S) là:
A. I - 2 ; - 2 ; - 8 ; R = 3
B. I - 1 ; - 1 ; - 4 ; R = 6
C. I - 1 ; - 1 ; - 4 ; R = 3
D. I - 1 ; - 1 ; - 4 ; R = 30 2
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
-
1
2
+
y
-
1
2
+
z
2
4
và một điểm M(2;3;1). Từ M kẻ được vô số các tiếp tuyến tới (S), biết tập hợp các tiếp điểm là đườ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x - 1 2 + y - 1 2 + z 2 = 4 và một điểm M(2;3;1). Từ M kẻ được vô số các tiếp tuyến tới (S), biết tập hợp các tiếp điểm là đường tròn (C). Tính bán kính r của đường tròn (C)
A. r = 2 3 3
B. r = 3 3
C. r = 2 3
D. r = 3 2
Chọn đáp án A
Mặt cầu (S) có tâm I(1;1;0) bán kính R = 2. Kẻ tiếp tuyến MA và MB sao cho M, A, I, B đồng phẳng suy ra đường tròn (C) là đường tròn đường kính AB.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
(
S
)
:
x
-
1
2
+
y
-
1
2
+...
Đọc tiếp
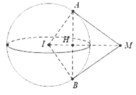
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu ( S ) : x - 1 2 + y - 1 2 + z 2 = 0 và một điểm M(2;3;1) Từ M kẻ được vô số các tiếp tuyến tới (S), biết tập hợp các tiếp điểm là đường tròn (C). Tính bán kính r của đường tròn (C).
A. r = 2 3 3
B. r = 3 3
C. r = 2 3
D. r = 3 2
Đáp án A.
Phương pháp giải: Dựng hình, xác định tập hợp tiếp điểm
Lời giải:
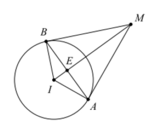
Xét mặt cầu ( S ) : x - 1 2 + y - 1 2 + z 2 = 0 có tâm I(1;1;0) bán kính R =2
Gọi A,B là các tiếp điểm. => E là tâm đường tròn (C), với bán kính r=EA (Hình vẽ bên).
Tam giác MAI vuông tại A, có
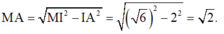
Suy ra
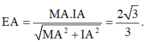
Vậy bán kính của (C) là r = 2 3 3
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
-
1
2
+
y
-
1
2
+
z
2
4
và một điểm M(2;3;1). Từ M kẻ được vô số các tiếp tuyến với (S), biết tập hợp các tiếp điểm là đườ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x - 1 2 + y - 1 2 + z 2 = 4 và một điểm M(2;3;1). Từ M kẻ được vô số các tiếp tuyến với (S), biết tập hợp các tiếp điểm là đường tròn (C). Tính bán kính r của đường tròn (C).
A. r = 2 3 3
B. r = 3 3
C. r = 2 3
D. r = 3 2
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
x
+
1
2
+
y
+
2
2
+
z
2...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : x + 1 2 + y + 2 2 + z 2 = 4 và các điểm A(-2;0;-2 2 ), B(-4;-4;0). Biết rằng tập hợp các điểm M thuộc (S) và thỏa mãn M A 2 + M O → . M B → = 16 là một đường tròn. Tính bán kính đường tròn đó.
A. 3 2 4 .
B. 3 2 .
C. 3 7 4 .
D. 5 2 .
Đáp án C
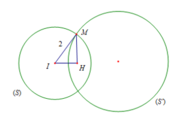
Bài giao hai mặt cầu:
Gọi M(x;y;z) theo bài M A 2 + M O → . M B → = 16
⇒ x + 2 2 + y 2 + ( z + 2 2 ) 2 + x ( x + 4 ) + y ( y + 4 ) + z 2 = 16
Giao tuyến của (S) và (S') là nghiệm của hệ phương trình:
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu (S):
(
x
+
1
)
2
+
(
y
+
2
)
2
+
z
2
4
và các điểm A(-2;0;-2...
Đọc tiếp
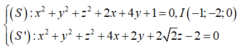
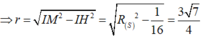
Trong không gian Oxyz, cho mặt cầu (S): ( x + 1 ) 2 + ( y + 2 ) 2 + z 2 = 4 và các điểm A(-2;0;-2 2 ), B(-4;-4;0). Biết rằng tập hợp các điểm M thuộc (S) và thỏa mãn MA 2 + MO → . MB → = 16 là đường tròn. Tính bán kính đường tròn đó.
A. 3 2 4
B. 3 2
C. 3 7 4
D. 5 2
Trong không gian Oxyz, cho điểm
M
2
;
-
3
;
4
. Gọi
P
là mặt phẳng đi qua M và cắt các trục
x
O
x
,
y
O
y
,
z
O
z
lần lượt tại các điểm D, E, F sao cho
O
D...
Đọc tiếp
Trong không gian Oxyz, cho điểm M 2 ; - 3 ; 4 . Gọi P là mặt phẳng đi qua M và cắt các trục x ' O x , y ' O y , z ' O z lần lượt tại các điểm D, E, F sao cho O D = 2 O E = m 2 - 2 m + 2 O F ≠ 0 , trong đó m là tham số thực. Gọi S là tập hợp các giá trị của m để chỉ có đúng ba mặt phẳng thỏa mãn yêu cầu trên.
Tập hợp S có bao nhiêu tập hợp con khác rỗng?
A. 7
B. 3
C. 15
D. 4
Chọn đáp án A.
Suy ra số tập hợp con khác rỗng của S là 2 3 - 1 = 7
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz cho hai điểm
A
l
;
0
;
−
3
,
B
−
3
;
−
2
;
−
5
.
Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho hai điểm A l ; 0 ; − 3 , B − 3 ; − 2 ; − 5 . Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức A M 2 + B M 2 = 30 là một mặt cầu (S). Tọa độ tâm I và bán kính R của mặt cầu (S) là
A. I − 2 ; − 2 ; − 8 ; R = 3
B. I − 1 ; − 1 ; − 4 ; R = 6
C. I − 1 ; − 1 ; − 4 ; R = 3
D. I − 1 ; − 1 ; − 4 ; R = 30 2
