Cho hình nón đỉnh S, đáy là đường tròn (O; r). Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho S A = A B = 8 r 5 . Tính theo r khoảng cách từ O đến (SAB).
A. 2 2 r 5
B. 3 13 r 20
C. 3 2 r 20
D. 13 r 20
Cho hình nón đỉnh S, đáy là hình tròn tâm O và có chiều cao bằng 40. Cắt hình nón bằng một mặt phẳng song song với mặt phẳng đáy, thiết diện thu được là đường tròn tâm O'. Chiều cao h của hình nón đỉnh S đáy là hình tròn tâm O' là. (biết thể tích của nó bằng 1/8 thể tích khối nón đỉnh S, đáy là hình tròn tâm O).
A. h=5
B. h=10
C. h=20
D. h=40
Cho hình nón đỉnh S, đáy là hình tròn tâm O và có chiều cao bằng 40. Cắt hình nón bằng một mặt phẳng song song với mặt phẳng đáy, thiết diện thu được là đường tròn tâm O'. Chiều cao h của khối nón đỉnh S đáy là hình tròn tâm O' bằng bao nhiêu, biết rằng thể tích của nó bằng 1 8 thể tích khối nón đỉnh S, đáy là hình tròn tâm O.
A. h = 5
B. h = 10
C. h = 20
D. h= 40
Cho hình nón đỉnh S, đáy là hình tròn tâm O và có chiều cao bằng 40. Cắt hình nón bằng một mặt phẳng song song với mặt phẳng đáy, thiết diện thu được là đường tròn tâm O'. Chiều cao h của khối nón đỉnh S đáy là hình tròn tâm O' bằng bao nhiêu, biết rằng thể tích của nó bằng 1 8 thể tích khối nón đỉnh S, đáy là hình tròn tâm O.
![]()
![]()
![]()
![]()
Cho hình nón N 1 đỉnh S đáy là đường tròn C(O;R), đường cao SO=40cm. Người ta cắt nón bằng mặt phẳng vuông góc với trục để được nón nhỏ N 2 có đỉnh S và đáy là đường tròn C'(O';R'). Biết rằng tỷ số thể tích V N 2 V N 1 = 1 8 . Tính độ dài đường cao nón N 2 .
![]()
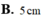
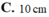
![]()
Cho hình nón đỉnh S, đáy là đường tròn (O; 5). Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho SA = AB = 8. Tính khoảng cách từ O đến (SAB).
![]()
![]()
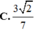
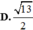
Cho hình nón đỉnh S, đáy là đường tròn (O; 5). Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho S A = A B = 8 . Tính khoảng cách từ O đến (SAB).
A. 2 2
B. 3 13 14
C. 3 2 7
D. 13 2
Chọn B.

Phương pháp: v
Cách giải: Gọi I là trung điểm AB, H là hình chiếu của O lên (SAB). Dễ dàng chứng minh
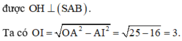
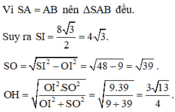
Cho hình nón đỉnh S, đáy là hình tròn tâm O, bán kính R=3cm, góc ở đỉnh hình nón là α = 120 ° . Cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A, B thuộc đường tròn đáy. Diện tích tam giác SAB bằng
A. 3 3 c m 2
B. 6 3 c m 2
C. 6 c m 2
D. 3 c m 2
Cho hình nón đỉnh S, đáy là hình tròn tâm O, bán kính R = 3cm, góc ở đỉnh hình nón là φ = 120 ° . Cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A, B thuộc đường tròn đáy. Diện tích tam giác SAB bằng:
A. 3 3 c m 2
B. 6 3 c m 2
C. 6 c m 2
D. 3 c m 2
Chọn đáp án A.
Góc ở đỉnh hình nón là φ = 120 ° là góc tạo bởi khi mặt phẳng đi qua trục SO => O S C ^ = 60 °
Khi cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB nên mặt phẳng không chứa trục của hình nón.
Xét tam giác vuông SOC tại O:
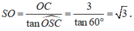
Xét tam giác vuông SOA tại O:
![]()
Do tam giác SAB đều:
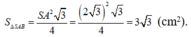
Cho hình nón đỉnh S, đáy là đường tròn (O,r). Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho SA=AB= 8 r 5 . Tính theo r khoảng cách từ O đến (SAB)
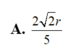
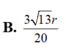
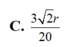
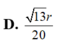
Cho hình nón đỉnh S, đáy là đường tròn (O;r). Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho SA = AB = 8 r 5 . Tính theo r khoảng cách từ O đến (SAB)
A. 2 2 r 5 .
B. 3 13 r 20 .
C. 3 2 r 20 .
D. 13 r 20 .