Cho cấp số cộng (Un) biết U1=; d=3
a) Cho Sn = 260. Tìm n
b) Tính S= U60 + U61 + U62 +... +U80
Những câu hỏi liên quan
Cho cấp số cộng
u
n
biết
u
1
3
,
u
2
-
1
. Tìm
u
3
A.
u
3
4
B.
u
3
2
C.
u
3...
Đọc tiếp
Cho cấp số cộng u n biết u 1 = 3 , u 2 = - 1 . Tìm u 3
A. u 3 = 4
B. u 3 = 2
C. u 3 = - 5
D. u 3 = 7
Chọn C.
Phương pháp
Công thức tổng quát của CSC có số hạng đầu là u1 và công sai d là: u n = u 1 + n - 1 d .
Tìm công sai d rồi suy ra u3.
Cách giải:
Đúng 0
Bình luận (0)
Cho cấp số cộng
(
u
n
)
biết
u
1
3
,
u
2
-
1
. Tìm
u...
Đọc tiếp
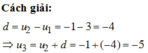
Cho cấp số cộng ( u n ) biết u 1 = 3 , u 2 = - 1 . Tìm u 3
A. u 3 = 4
B. u 3 = 2
C. u 3 = -5
D. u 3 = 7
Chọn C.
Phương pháp
Công thức tổng quát của CSC có số hạng đầu là u1 và công sai d là:
u n = u 1 + ( n - 1 ) d
Tìm công sai d rồi suy ra u3
Đúng 0
Bình luận (0)
Cho cấp số cộng
(
u
n
)
biết
u
5
18
và
4
S
n
S
2
n
. Tìm số...
Đọc tiếp
Cho cấp số cộng ( u n ) biết u 5 = 18 và 4 S n = S 2 n . Tìm số hạng đầu tiên u 1 và công sai d của cấp số cộng
A. u 1 = 3 ; d = 2
B. u 1 = 2 ; d = 3
C. u 1 = 2 ; d = 2
D. u 1 = 2 ; d = 4
Đáp án D
u 5 = 18 ⇔ u 1 + 4 d = 18 ( 1 )
4 S n = S 2 n
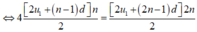
⇒ 2 u 1 - d = 0 ( 2 )
Từ (1) & (2) ta có u 1 = 2 ; d = 2
Đúng 0
Bình luận (0)
Cho cấp số cộng
(
u
n
)
biết
u
5
18
v
à
4
S
n
S
2
n
. Tìm số hạng đầu tiên
u
1
và công sai d của cấp số cộng A.
u
1
2
,
d
4...
Đọc tiếp
Cho cấp số cộng ( u n ) biết u 5 = 18 v à 4 S n = S 2 n . Tìm số hạng đầu tiên u 1 và công sai d của cấp số cộng
A. u 1 = 2 , d = 4
B. u 1 = 2 , d = 3
C. u 1 = 2 , d = 2
D. u 1 = 3 , d = 2
Cho cấp số cộng
u
n
biết
u
5
18
và
4
S
n
S
2
n
.
Tìm số hạng đầu tiên
u
1
và công sai d của cấp số cộng. A.
u
1
2
,...
Đọc tiếp
Cho cấp số cộng u n biết u 5 = 18 và 4 S n = S 2 n . Tìm số hạng đầu tiên u 1 và công sai d của cấp số cộng.
A. u 1 = 2 , d = 4
B. u 1 = 2 , d = 3
C. u 1 = 2 , d = 2
D. u 1 = 3 , d = 2
Tìm cấp số cộng
(
u
n
)
biết
u
1
+
u
2
+
.
....
Đọc tiếp
Tìm cấp số cộng ( u n ) biết u 1 + u 2 + . . . + u n = a u 1 2 + u 2 2 + . . . . + u n 2 = b 2
Ta có
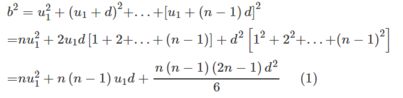
Mặt khác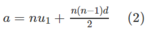 
Từ (2) tìm được u 1 thay u 1 vào (1) đểm tìm d.
Kết quả
Đúng 0
Bình luận (0)
Cho cấp số cộng
u
n
, biết u1 -1, d 3. Khi đó u13 bằng A. -531441 B. 38 C. 35 D. -1594323
Đọc tiếp
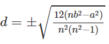
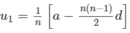
Cho cấp số cộng u n , biết u1 = -1, d = 3. Khi đó u13 bằng
A. -531441
B. 38
C. 35
D. -1594323
Cho cấp số cộng
u
n
có
u
1
+
2
u
5
0
và
S
4
14
. Tính số hạng đầu
u
1
và công sai d của cấp số cộng. A.
u
1...
Đọc tiếp
Cho cấp số cộng u n có u 1 + 2 u 5 = 0 và S 4 = 14 . Tính số hạng đầu u 1 và công sai d của cấp số cộng.
A. u 1 = 8 ; d = 3
B. u 1 = - 8 ; d = 3
C. u 1 = - 8 ; d = - 3
D. u 1 = 8 ; d = - 3
Cho cấp số cộng
u
n
, biết
u
1
-
5
,
d
2
. Số 81 là số hạng thứ bao nhiêu? A. 44 B. 100 C. 75 D. 50
Đọc tiếp
Cho cấp số cộng u n , biết u 1 = - 5 , d = 2 . Số 81 là số hạng thứ bao nhiêu?
A. 44
B. 100
C. 75
D. 50
Cho cấp số cộng
u
n
, biết
u
1
-
5
,
d
2
. Số 81 là số hạng thứ bao nhiêu? A. 44 B. 100 C. 75 D. 50
Đọc tiếp
Cho cấp số cộng u n , biết u 1 = - 5 , d = 2 . Số 81 là số hạng thứ bao nhiêu?
A. 44
B. 100
C. 75
D. 50
Ta có: u n = u 1 + ( n - 1 ) d hay 81 = - 5 + n - 1 . 2 ⇔ n = 44
Vậy 81 là số hạng thứ 44 của dãy.
Chọn đáp án A.
Đúng 0
Bình luận (0)