Cho a/b = b/c = c/a và a+b+c không bằng 0 ; a= 2015
Tính b và c ?
Những câu hỏi liên quan
cho 3 số a,b,c khác 0 và a+b+c không bằng 0 thỏa mãn điều kiện a/b+c =b/a+c = c/a+b
tính giá trị biểu thức P=b+c/a + a+c/b + a+b/c
Cho a,b,c không bằng 0 và a+b+c không bằng 0 thỏa mãn \(\frac{-a+b+c}{a}\)=\(\frac{a-b+c}{b}\)=\(\frac{a+b-c}{c}\)
Tính \(\frac{\left(a+b\right).\left(b+c\right).\left(c+a\right)}{abc}\)
Áp dụng tính chất dãy tỷ số bằng nhau ta đc\(\frac{-a+b+c}{a}=\frac{a-b+c}{b}=\)\(\frac{a+b-c}{c}=\frac{a+b+c}{a+b+c}=1\)
Dễ dàng cm đc \(a=b=c\)tính đc P=8
Trong không gian Oxyz, cho hình vuông ABCD có A(8; 0; 3),C(0; -4; -5) và
D
(
a
;
b
;
c
)
(
a
;
b
;
c
∈
ℤ
)
thuộc mặt phẳng (Oyz). Giá trị a + b + c bằng A. -3 B. -2 C. 2 D. 3
Đọc tiếp
Trong không gian Oxyz, cho hình vuông ABCD có A(8; 0; 3),C(0; -4; -5) và D ( a ; b ; c ) ( a ; b ; c ∈ ℤ ) thuộc mặt phẳng (Oyz). Giá trị a + b + c bằng
A. -3
B. -2
C. 2
D. 3
Có I(4;-2;1) là trung điểm AC. Ta có hệ điều kiện:
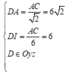
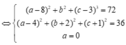
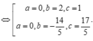
Đối chiếu điều kiện a ; b ; c ∈ ℤ ⇒ a = 0 , b = 2 , c = 1 và a+b+c=0+2+1=3
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho 1/c = 1/2 (1/a + 1/b (với a,b,c không bằng 0 , b không bằng c) chứng minh rằng a/b = a-c/c-b
Câu hỏi của nguyen thanh chuc - Toán lớp 7 - Học toán với OnlineMath
biết 1/c = 1/2.(1/a+1/b) và abc không bằng 0; b không bằng c; chứng minh rằng: a/b = (a-c)/(c-b)
Câu hỏi của nguyen thanh chuc - Toán lớp 7 - Học toán với OnlineMath
Cho a/b=b/c=a/c và a+b+c khác 0 .Tinh M=(a^2.b^3.c^2030)/b^2030
các bạn ghi ra giấy bằng cách khác cho dễ giải nhé mình không biết ghi
1.a)Cho các số dương a,b,c có tích bằng 1.Chứng minh rằng (a+1)(b+1)(c+1) lớn hơn hoặc bằng 8.
b)Chocacs số a và b không âm.Chứng minh rằng (a+b)(ab+1) lớn hơn hoặc bằng 4ab.
2.Cho các số dương a,b,c,d có tích bằng 1.Chứng minh rằng a bình +b bình +c bình +d bình +ab+cd lớn hơn hoặc bằng 6.
3.Chứng minh rằng nếu a+b+c>0.abc>0.ab+bc+ca>0 thì a>0,b>0,c>0.
3. abc > 0 nên trog 3 số phải có ít nhất 1 số dương.
Vì nếu giả sử cả 3 số đều âm => abc < 0 => trái giả thiết
Vậy nên phải có ít nhất 1 số dương
Không mất tính tổng quát, giả sử a > 0
mà abc > 0 => bc > 0
Nếu b < 0, c < 0:
=> b + c < 0
Từ gt: a + b + c < 0
=> b + c > - a
=> (b + c)^2 < -a(b + c) (vì b + c < 0)
<=> b^2 + 2bc + c^2 < -ab - ac
<=> ab + bc + ca < -b^2 - bc - c^2
<=> ab + bc + ca < - (b^2 + bc + c^2)
ta có:
b^2 + c^2 >= 0
mà bc > 0 => b^2 + bc + c^2 > 0
=> - (b^2 + bc + c^2) < 0
=> ab + bc + ca < 0 (vô lý)
trái gt: ab + bc + ca > 0
Vậy b > 0 và c >0
=> cả 3 số a, b, c > 0
Đúng 0
Bình luận (0)
1.a, Ta có: \(\left(a+b\right)^2\ge4a>0\)
\(\left(b+c\right)^2\ge4b>0\)
\(\left(a+c\right)^2\ge4c>0\)
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64abc\)
Mà abc=1
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\left(đpcm\right)\)
Đúng 0
Bình luận (0)
sai rồi. sửa a+b=a+1, b+c=b+1, a+c=c+1 nha, thông cảm, nhìn sai đề
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho các điểm A(2 ;1 ;0),B(0 ;4 ;0),C(0,2,-1) Biết đường thẳng ∆ vuông góc với mặt phẳng (ABC) và cắt đường thẳng
d
:
x
-
1
2
y
+
1
1
z
-
2
3
tại điểm D(a ;b ;c) thỏa mãn a 0 và tứ di...
Đọc tiếp
Trong không gian Oxyz, cho các điểm A(2 ;1 ;0),B(0 ;4 ;0),C(0,2,-1) Biết đường thẳng ∆ vuông góc với mặt phẳng (ABC) và cắt đường thẳng d : x - 1 2 = y + 1 1 = z - 2 3 tại điểm D(a ;b ;c) thỏa mãn a > 0 và tứ diện ABCD có thể tích bằng 17/6. Tổng a+b+c bằng
A. 5
B. 4
C. 7
D. 6
cho a^2=bd ; b^2 = ac ; a+b+c không bằng 0;a^3+b^3+c^3 không bằng 0 cmr :\(\frac{d}{c}\)=\(\frac{a^3+b^3+c^3}{b^3+c^3+a^3}\)=\(\frac{\left(a+b+c\right)^3}{\left(b+c+a\right)^3}\)