Cho hình chóp S.ABC có thể tích V. Gọi M, N, P là các điểm thỏa mãn S A = 2 S M ; S B = 2 S N ; S C = 1 2 S P Tính thể tích của khối chóp S.MNP theo V.
A. V 3
B. V 4
C. V 2
D. V 5
Cho hình chóp S.ABC có thể tích V. Gọi M, N, P là các điểm thỏa mãn SA = 2SM; SB = 2SN; SC = 1 2 SP. Tính thể tích của khối chóp S.MNP theo V.
A . V 3
B . V 4
C . V 2
D . V 5
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB=2a và B C = 2 a 3 . Gọi M là trung điểm của BC, hình chiếu vuông góc của S xuống mặt phẳng đáy là điểm nằm trên AM thỏa mãn A H → = 2 H M → . Góc giữa hai mặt phẳng (SAB) và (ABC) bằng 45 ° . Thể tích khối chóp S.ABC là
A. 8 a 3 3 3
B. 8 a 3 3 9
C. 8 a 3 3
D. 8 a 3 9
Cho hình chóp S.ABC. Lấy M, N, P lần lượt thuộc các cạnh SA, SB, SC thỏa mãn Biết thể tích S.ABC là a 3 2 Thể tích hình chóp S.MNP là
A. a 3 4
B. 2 a 3 7
C. a 3 24
D. a 3 16
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AB = a. Gọi I là trung điểm của AC. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là điểm H thỏa mãn B I → = 3 I H → . Góc giữa hai mặt phẳng (SAB) và (SBC) là 60 độ. Thể tích của khối chóp S.ABC là:
A. V = a3/9
B.V = a3/6
C.V = a3/18
D.V = a3/3
Chọn A
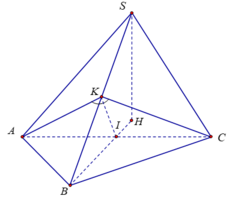
Cách 1:
Dễ thấy hai tam giác SAB và SAC bằng nhau (cạnh chung SA), gọi K là chân đường cao hạ từ A trong tam giác SAB
![]()
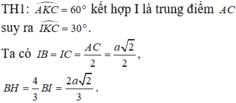
Từ giả thiết tam giác ABC vuông cân tại B ta được ![]()
Trong tam giác ICK vuông tại I có 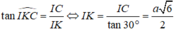 .
.
Như vậy Ik > IB (vô lý).
TH2: ![]() tương tự phần trên ta có
tương tự phần trên ta có 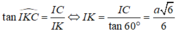
Do ![]() nên tam giác BIK vuông tại K và
nên tam giác BIK vuông tại K và 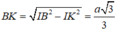
Như vậy tam giác BKI đồng dạng với tam giác BHS suy ra: ![]()
Vậy thể tích của khối chóp S.ABC là 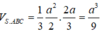
Cách 2: dùng phương pháp tọa độ hóa.
Cho hình chóp S.ABC có thể tích V. M, N, P là các điểm trên tia SA, SB, SC thoả mãn S M = 1 4 S A , S N = 1 3 S B , S P = 3 S C Thể tích của khối chóp S.MNP theo V
A. V 5
B. V 4
C. V 3
D. V 2
Cho hình chóp S.ABC. Lấy M, N, P lần lượt thuộc các cạnh SA, SB, SC thỏa mãn S A = 2 S M , S B = 3 S N , S C = 2 S P Biết thể tích S.ABC là a 3 2 Thể tích hình chóp S.MNP là
A. a 3 4
B. 2 a 3 7
C. a 3 24
D. a 3 16
Đáp án C
Ta có:
V S . M N P V S . A B C = S M S A . S N S B . S P S C = 1 12
⇒ V S . M N P = a 3 24
Cho hình chóp S.ABC có thể tích V. M, N, P là các điểm trên tia SA, SB, SC thoả mãn SM = 1 4 SA, SN = 1 3 SB, SP = 3SC. Thể tích của khối chóp S.MNP theo V
A . V 5
B . V 4
C . V 3
D . V 2
Đáp án là B
Theo công thức tỉ số thể tích của hình chóp tam giác ta có
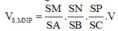
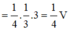
Cho hình chóp S.ABC có tam giác ABC và tam giác SAB là tam giác đều. hình chiếu vuông góc của S trên (ABC) là trung điểm của của AB. SC = (a căn6)/2, gọi M là trung điểm của SC. tính thể tích khối chóp S.ABC và tính khoảng cách giữa AM với SB
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB=a , AB vuông góc với SA , BC vuông góc với SC . Gọi M,N lần lượt là trung điểm SC,AC . Góc giữa hai mặt phẳng (BMN) và (SAB) là a thỏa mãn cosa= \(\dfrac{\sqrt{5}}{3}\).Thể tích khối chóp S.BMN bằng bao nhiêu?