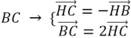Tam giác ABC cân ở A , 2 đường cao ; BE,CF cắt nhau ở I.
a,Chứng minh AE=CF, tam giác AEF là tam giác gì?
b, Chứng minh AI phân giác góc A
c, Chứng minh EF song song BC
Cho tam giác ABC cân ở A,đường cao BH=5cm,ABH=30độ .Giải tam giác ABC
Tam giác ABH vuông tại H, có góc ABH = 300
=> góc A = 600
mà tam giác ABC cân tại A
=> tam giác ABC đều
=> góc B = góc C = 600
\(\tan A=\tan60^0=\frac{BH}{AH}=\sqrt{3}\)
=> \(AH=\frac{BH}{\sqrt{3}}=\frac{5}{\sqrt{3}}\)
do tam giác ABC đều, BH là đường cao
=> BH đồng thời là trung tuyến
=> \(AC=\frac{10}{\sqrt{3}}\)
Vậy \(AB=AC=BC=\frac{10}{\sqrt{3}}\); \(\widehat{A}=\widehat{B}=\widehat{C}=60^0\)
cho tam giác ABC cân ở A , góc B = 65 độ , đường cao CH = 3,6 . Hãy giải tam giác ABC
1. Cho tam giác ABC vuông tại A có AC=1cm, BC=2cm. Kẻ đường trung tuyến BK và đường cao AH
a) Tính AB
b) Tính BK và AH
2. Cho tam giác ABC vuông cân tại A (ˆBAC=90BAC^=90 độ, BD=BA). Ở phía ngoài tam giác ABC, dựng tam giác DAB vuông cân tại D (ˆDAB=90DAB^=90 độ, BD=BA). Gọi E là một điểm tùy ý trên DA. Đường thẳng đi qua E và vuông góc với BE cắt AC ở F
a) Gọi K là giao điểm của BD và AC. CMR tam giác KAB vuông cân tại A và DA là đường trung trực của đoạn KB
b) CMR tam giác KEA= tam giác BEA
c) CMR tam giác KEF cân tại E. Từ đó suy ra BE= EF
Ở phía ngoài tam giác ABC vẽ tam giác ACE vuông cân tại C . Đường cao AH của tam giác ABC và đường cao CK của tam giác BCE . Hai đường cao cắt nhau tại N. Chứng minh AN =BC
Bài 4: Cho tam giác ABC vuông cân tại A, BC=2cm. Ở phía ngoài tam giác ABC vẽ tam giác ACE vuông cân tại E.
a) Chứng minh rằng EC vuông góc với BC
b) Tính số đo các góc của tứ giác ABCE.
Bài 5: Cho tam giác ABC vuông ở A, AH là đường cao, M là một điểm trên BC sao cho CM=CA. Đường thẳng đi qua M song song với CA cắt AB tại I.
a) Chứng minh AM là phân giác của góc BAH
b) Chứng minh rằng luôn luôn có AB+AC< AH+BC
Mình đang cần gấp bài này. Các bạn giúp mình nhé cảm ơn các bạn nhiều.
Bài 4:
a) Ta có tam giác ABC vuông cân tại A, nên góc BAC = 45 độ. Vì tam giác ACE vuông cân tại E, nên góc CAE = 45 độ. Từ đó suy ra góc CAE + góc BAC = 90 độ, tức là EC vuông góc với BC.
b) Vì tam giác ABC vuông cân tại A, nên góc BAC = 45 độ. Vì tam giác ACE vuông cân tại E, nên góc CAE = 45 độ. Từ đó suy ra góc BAE = góc BAC + góc CAE = 45 độ + 45 độ = 90 độ. Do đó, tứ giác ABCE là tứ giác vuông.
Bài 5:
a) Gọi K là giao điểm của đường thẳng AM và BH. Ta cần chứng minh góc BAK = góc CAK.
Vì CM = CA, ta có góc CMA = góc CAM. Vì đường thẳng AM song song với CA, nên góc CMA = góc KAB (do AB cắt đường thẳng AM tại I). Từ đó suy ra góc CAM = góc KAB.
Vì AH là đường cao, nên góc BAH = góc CAH. Từ đó suy ra góc BAK = góc CAK.
Vậy, AM là phân giác của góc BAH.
b) Ta có AB + AC = AB + AH + HC = BH + HC > BC (theo bất đẳng thức tam giác).
Vậy, luôn luôn có AB + AC < AH + BC.
Cho tam giác ABC cân ở A, có đường cao AH = 32cm, đường cao BK = 38,4cm
a) Tính các cạnh của tam giác ABC
b) Đường trung trực của AC cắt AH tại O. Tính OH ?
Cho tam giác ABC cân ở A, đường cao AD, phân giác AE, Tính các góc của tam giác, biết BE = 2AD.
Tam giác ABC cân ở A, 2 đường cao BD và CE cắt nhau ở I (D thuộc AC, E thuộc AB). Tia AI cắt BC ở M. C/m:
a, M là trung điểm của BC.
b,Tam giác MED cân
A) Ta có hai đường cao BD và CE giao nhau tại điểm I nên điểm I là trực tâm của tam giác ABC
Mà ta lại có AM đi qua I vậy AM là đường cao của tam giác ABC
Ta lại có tính chất đường cao nối từ đỉnh cân tới cạnh đối diện trong tam giác cân vừa là đường cao vừa là đường trung trực của cạnh đối điện mad đường cao đó đi qua
Vậy M là trung điểm của BC ( CMT)
B) Cái này dài lắm mik gợi ý nhé Cm : AM là đường trung trục của ED từ đó suy ra ME=MD
Bài 3:Cho tam giác ABC cân ở A, có AB=AC=100cm, BC=120 cm hai đường cao AD, BE cắt nhau ở H
a)Tìm các tam giác đồng dạng với tam giác BDH
b)Tính độ dài các đoạn HD, AH, BH, HE
Bài 5:Cho tam giác ABC vuông tại A đường cao AH
a)Chứng minh rằng AB2 =BH.BC và AC2 =CH.CB
b)Tính chu vi tam giác ABC, nếu BH= 9cm, HC= 16 cm
Cho tam giác ABC cân ở A, đường cao AH. Khẳng định nào sau đây sai?
![]()
![]()
![]()
![]()
Chọn A.
Tam giác ABC cân tại A, đường cao AH. Do đó, H là trung điểm BC.
Ta có:
+ tam giác cân tại A nên ![]()
+ Do H là trung điểm