Chọn B

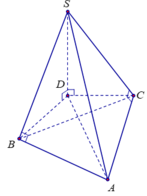
Gọi D là hình chiếu của S lên mặt phẳng (ABC), suy ra  S D ⊥ A B C .

Ta có  S D ⊥ A B  và  S B ⊥ A B ( g t ) , suy ra  A B ⊥ S B D ⇒ B A ⊥ B D .

Tương tự có  A C ⊥ D C  hay tam giác ACD vuông ở C.

Dễ thấy  ∆ S B A = ∆ S C A  (cạnh huyền và cạnh góc vuông), suy ra SB=SC. Từ đó ta chứng minh được  ∆ S B D = ∆ S C D  nên cũng có DB=DC.

Vậy DA là đường trung trực của BC, nên cũng là đường phân giác của góc  B A C ^ .

Ta có  D A C ^ = 30 o , suy ra  D C = a 3 . Ngoài ra góc giữa hai mặt phẳng (SAB) và (ABC) là  S B D ^ = 60 o  suy ra  tan S B D ^ = S D B D ⇒ S D = B D tan S B D ^ = a 3 . 3 = a
Vậy V S . A B C = 1 3 . S ∆ A B C . S D = 1 3 a 2 3 4 . a = a 3 3 12

a) Xét \(\Delta HAC\) và \(\Delta ABC\) có :

Góc AHC = góc BAC = 90^o; góc C chung

=> \(\Delta HAC\) đồng dạng với \(\Delta ABC\) (g.g)

b) Vì \(\Delta ABC\) vuông tại A nên AB² + AC² = BC² => AB² = BC² - AC² = 20² - 16² = 144

=> \(AB=\sqrt{144}=12\left(cm\right)\)

Từ a) => \(\frac{AH}{AB}=\frac{AC}{BC}\) hay \(\frac{AH}{6}=\frac{8}{10}\) => \(AH=\frac{6.8}{10}=4,8\left(cm\right)\)

c) Ta có \(\Delta ABD\) đồng dạng với \(\Delta HBI\) (g.g) ('Bạn tự chứng minh')

=> Góc BIH = góc ADB

Mà góc BIH = góc AID (đ²) => Góc AID = góc ADB

=> Tam giác AID cân tại A

d) ('Mình ko biết')

a) Xét \(\Delta HAC\) và \(\Delta ABC\) có :

Góc AHC = góc BAC = 90^o; góc C chung

=> \(\Delta HAC\) đồng dạng với \(\Delta ABC\) (g.g)

b) Vì \(\Delta ABC\) vuông tại A nên AB² + AC² = BC² => AB² = BC² - AC² = 20² - 16² = 144

=> \(AB=\sqrt{144}=12\left(cm\right)\)

Từ a) => \(\frac{AH}{AB}=\frac{AC}{BC}\) hay \(\frac{AH}{6}=\frac{8}{10}\) => \(AH=\frac{6.8}{10}=4,8\left(cm\right)\)

c) Ta có \(\Delta ABD\) đồng dạng với \(\Delta HBI\) (g.g) ('Bạn tự chứng minh')

=> Góc BIH = góc ADB

Mà góc BIH = góc AID (đ²) => Góc AID = góc ADB

=> Tam giác AID cân tại A