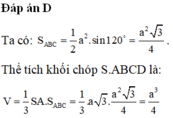Cho khối chóp S.ABC có đáy là tam giác cân, AB = AC=5a; BC = 6a và các mặt bên tạo với đáy một góc \(60^0\). Hãy tính thể tích của khối chóp đó ?

Những câu hỏi liên quan
Cho khối chóp S.ABC có đáy là tam giác cân, AB = AC = 5a, BC = 6a và các mặt bên tạo với đáy một góc 60 ° . Hãy tính thể tích của khối chóp đó.
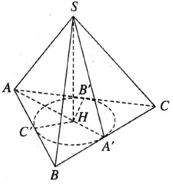
Kẻ SH ⊥ (ABC) và HA’, HB’ , HC’ lần lượt vuông góc với BC, CA, AB. Theo định lí ba đường vuông góc ta có SA′ ⊥ BC, SB′ ⊥ CA, SC′ ⊥ AB
Từ đó suy ra ∠ SA′H = ∠ SB′H = ∠ SC′H = 60 ° .
Do đó các tam giác vuông SHA’ , SHB’ , SHC’ bằng nhau. Từ đó suy ra HA’ = HB’ = HC’ . Vậy H là tâm đường tròn nội tiếp tam giác ABC. Do tam giác cân ở A nên AH vừa là đường phân giác , vừa là đường cao, vừa là đường trung tuyến. Từ đó suy ra A, H, A’ thẳng hàng và A’ là trung điểm của BC.
Do đó, AA ' 2 = AB 2 - BA ' 2 = 25 a 2 - 9 a 2 = 16 a 2
Vậy AA’ = 4a
Gọi p là nửa chu vi của tam giác ABC, r là bán kính đường tròn nội tiếp của nó.
Khi đó SABC = 6a.4a/2 = 12a2 = pr = 8ar
Từ đó suy ra r = 3a/2
Do đó
![]()
Thể tích khối chóp là:
![]()
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, AB AC a; mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC A.
1
12
a
3
B.
3
4
a
3
C.
3
12...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, AB = AC= a; mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC
A. 1 12 a 3
B. 3 4 a 3
C. 3 12 a 3
D. 1 4 a 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân,
A
B
A
C
a
; mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC. A.
1
12
a
3
B.
3
4
a
3
C. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, A B = A C = a ; mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC.
A. 1 12 a 3
B. 3 4 a 3
C. 3 12 a 3
D. 1 4 a 3
Đáp án A
Gọi H là trung điểm của AB suy ra S H ⊥ A B
Do Δ S A B vuông cân tại S nên S H = A B 2 = a 2 ; S A B C = a 2 2 ⇒ V = a 3 12 .
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác cân tại A,
A
B
A
C
a
;
B
A
C
120
°
. Tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối chóp S.ABC. A.
V
a
3
B.
V
a
3
2...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác cân tại A, A B = A C = a ; B A C = 120 ° . Tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối chóp S.ABC.
A. V = a 3
B. V = a 3 2
C. V = 2 a 3
D. V = a 3 8
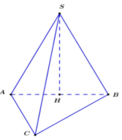
Gọi H là trung điểm của AB.
∆ S A B đều và nằm trong mặt phẳng vuông góc với
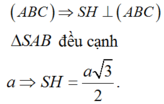
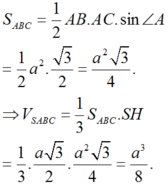
Chọn D.
Đúng 0
Bình luận (0)
Cho hình chóp tam giác S.ABC có đáy là tam giác cân ABACa, góc BAC bằng 1200, cạnh bên và vuông góc với mặt phẳng đáy. Tính theo a thể tích của khối chóp S.ABC. A.
3
12
a
3
B.
3
4
a
3
C.
3
4
a
3
D.
1...
Đọc tiếp
Cho hình chóp tam giác S.ABC có đáy là tam giác cân AB=AC=a, góc BAC bằng 1200, cạnh bên và vuông góc với mặt phẳng đáy. Tính theo a thể tích của khối chóp S.ABC.
A. 3 12 a 3
B. 3 4 a 3
C. 3 4 a 3
D. 1 4 a 3
Đáp án D
S A B C = A B . A C . sin B A C ^ 2 = a 2 3 4
Vì SA vuông góc với mặt phẳng đáy nên suy ra
V
S
.
A
B
C
=
1
3
.
S
A
.
S
A
B
C
=
1
3
.
a
3
.
a
2
3
4
=
1
4
a
3
Đúng 0
Bình luận (0)
Cho hình chóp tam giác S.ABC có đáy là tam giác cân AB AC a, góc BAC bằng
120
0
cạnh bên
S
A
a
3
và vuông góc với mặt phẳng đáy. Tính theo a thể tích của khối chóp S.ABC A.
3
a
3
12
B.
3...
Đọc tiếp
Cho hình chóp tam giác S.ABC có đáy là tam giác cân AB =AC =a, góc BAC bằng 120 0 cạnh bên S A = a 3 và vuông góc với mặt phẳng đáy. Tính theo a thể tích của khối chóp S.ABC
A. 3 a 3 12
B. 3 a 3 4
C. 3 a 3 4
D. 1 4 a 3
Cho hình chóp tam giác S.ABC có đáy là tam giác cân
A
B
A
C
a
,
góc BAC bằng
120
°
cạnh bên
S
A
a
3
và vuông góc với mặt phẳng đáy. Tính theo a thể tích của khối chóp S.ABC. A.
3
12
a
3
B.
3...
Đọc tiếp
Cho hình chóp tam giác S.ABC có đáy là tam giác cân A B = A C = a , góc BAC bằng 120 ° cạnh bên S A = a 3 và vuông góc với mặt phẳng đáy. Tính theo a thể tích của khối chóp S.ABC.
A. 3 12 a 3
B. 3 4 a 3
C. 3 4 a 3
D. 1 4 a 3
Đáp án D
Ta có: S A B C = 1 2 a 2 . sin 120 ∘ = a 2 3 4 .
Thể tích khối chóp S.ABCD là: V = 1 3 S A . S A B C = 1 3 . a 3 . a 2 3 4 = a 3 4
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác cân tại A,
A
B
A
C
a
,
B
A
C
^
120
0
. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Thể tích V của khối chóp S.ABC là A.
V
a
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác cân tại A, A B = A C = a , B A C ^ = 120 0 . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Thể tích V của khối chóp S.ABC là
A. V = a 3 8 .
B. V = a 3 .
C. V = a 3 2 .
D. V = 2 a 3 .
Đáp án A
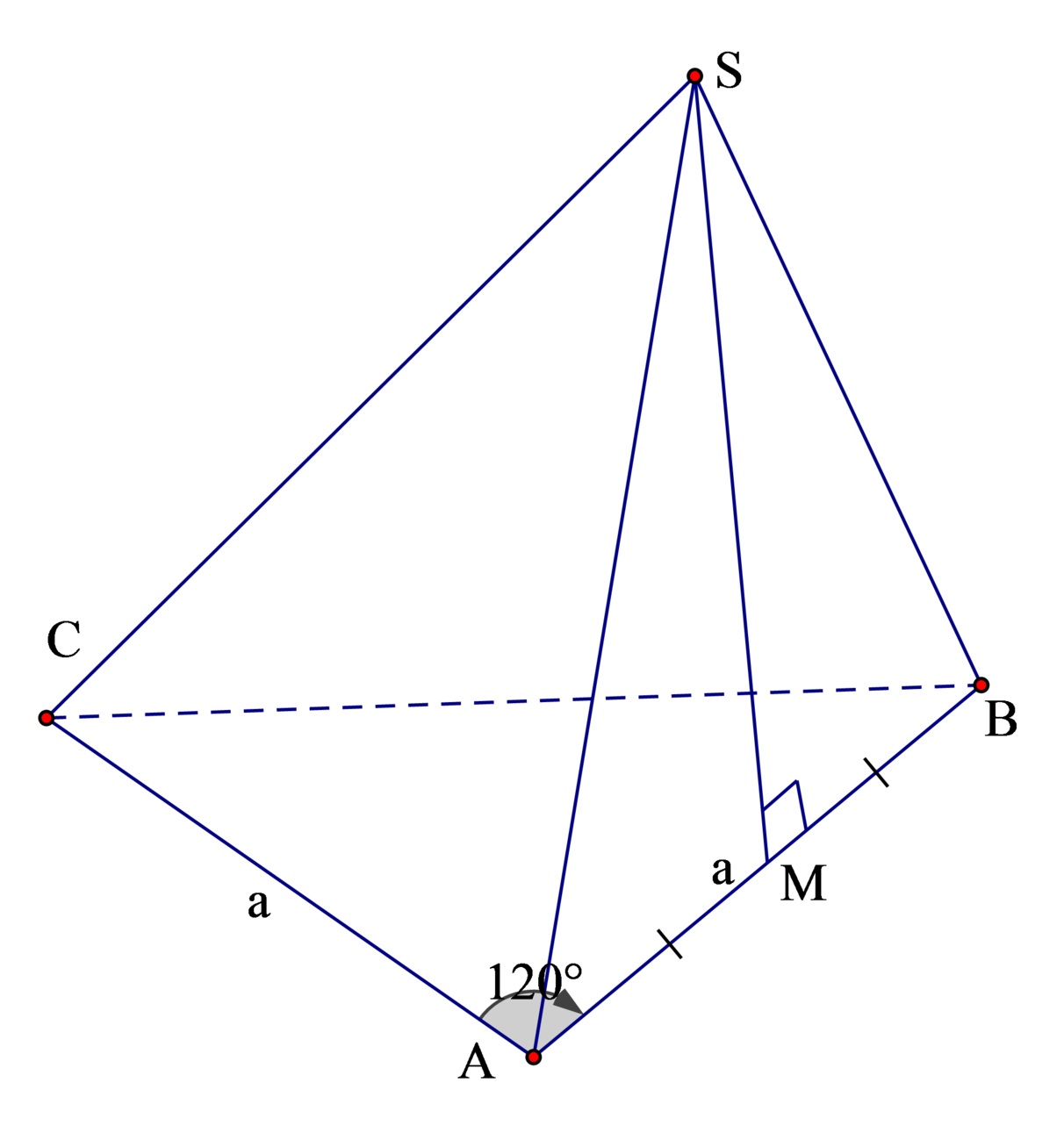
Gọi M là trung điểm AB khi đó S M ⊥ A B ⇒ S M ⊥ A B C
Ta có: S M = a 3 2 (độ dài đường cao trong tam giác đều);
d t A B C = 1 2 A B . A C . sin 120 0 = 3 4 a 2
Vậy thể tích của khối chop là:
V S . A B C = 1 3 S M . d t A B C = 1 3 a 3 2 a 2 3 4 = a 3 8
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác cân tại A, ABACa, BAC
120
o
. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Thể tích V của khối chóp S.ABC là
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác cân tại A, AB=AC=a, BAC= 120 o . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Thể tích V của khối chóp S.ABC là
![]()
![]()