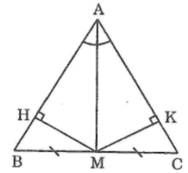
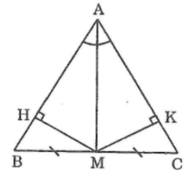
Cho tam giác AVC có M là trung điểm của BC và AM là tia phân giác của góc A kẻ MH vuông góc AB, Mk vuông góc AC. Chứng minh rằng :
a, MH = MK ; AH = AK
b, Tam giác ABC cân
c, HK song song BC
Giúp mk nha mấy chế !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!