tam giác ABC. ở phía ngoài tam giác ABC vẽ các tam giác vuông ABD ; ACE ( vuông cân tại B, tai C). kẻ DI và EK vuông góc BC , I,K thuộc BC. chứng minh BI=CK

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A vẽ tam giác đều ABD ở phía ngoài tam giác ABC .Tính số đo các góc của tam giác BDC
chiu roi
ban oi
tk nhe@@@@@@@@@@@!!
ai tk minh minh tk lai
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông cân tại A ở phía ngoài tam giác ABC Vẽ tam giác đều ABD tính số đo các góc của tam giác bdc
Tam giác ABC có ^BAC= 90; ^ABC=^ACB=45
Tam giác ABD có ^ABC=^BAC=^ACB=60
=> Tam giác BDC có
^CBD=60-45=15
Cho tam giác vuông cân tại A. Vẽ tam giác đều ABD ở phía ngoài tam giác ABC . Tính số đo các góc của tam giác BDC
cho tam giác ABC có đường cao AH vẽ phía ngoài tam giác ABC các tam giác vuông cân ABD vàACE
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ các tam giác ABD vuông cân tại A, vẽ tam giác ABD vuông cân tại A, vẽ tam giác ACE vuông cân tại E. CMR: Tứ giác BDEC là hình thang cân
Cho tam giác ABC. Ở phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Vẽ hình bình hành ADIE. Chứng minh rằng: IA = BC
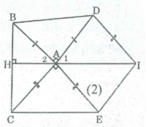
∠ (BAD) + ∠ (BAC) + ∠ (DAE) + ∠ (EAC) = 360 0
Lại có: ∠ (BAD) = 90 0 , ∠ (EAC) = 90 0
Suy ra: ∠ (BAC) + ∠ (DAE) = 180 0 (1)
AE // DI (gt)
⇒ ∠ (ADI) + ∠ (DAE) = 180 0 (2 góc trong cùng phía)
Từ (1) và (2) suy ra: ∠ (BAC) = ∠ (ADI)
Xét ∆ ABC và ∆ DAI có:
AB = AD ( vì tam giác ABD vuông cân).
AC = DI ( = AE)
∠ (BAC) = ∠ (ADI) ( chứng minh trên)
Suy ra: ∆ ABC = ∆ DAI (c.g.c) ⇒ IA = BC
Đúng 0
Bình luận (0)
Cho tam giác ABC. Ở phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Vẽ hình bình hành ADIE. Chứng minh rằng: IA ⊥ BC
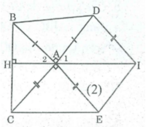
∆ ABC = ∆ DAI (chứng minh trên) ⇒ ∠ (ABC) = ∠ A 1 (3)
Gọi giao điểm IA và BC là H.
Ta có: ∠ A 1 + ∠ (BAD) + ∠ A 2 = 180 0 (kề bù)
Mà ∠ (BAD) = 90 0 (gt) ⇒ ∠ A 1 + ∠ A 2 = 90 0 (4)
Từ (3) và (4) suy ra: ∠ (ABC)+ ∠ A 2 = 90 0
Trong ∆ AHB ta có: ∠ (AHB) + ∠ (ABC)+ ∠ A 2 = 180 0
Suy ra ∠ (AHB) = 90 0 ⇒ AH ⊥ BC hay IA ⊥ BC
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM 1/2 DE và AM vuông góc DECho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM 1/2 DE và AM vuông góc DECho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM 1/2 DE và AM vuông góc DE
Đọc tiếp
Cho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM = 1/2 DE và AM vuông góc DECho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM = 1/2 DE và AM vuông góc DECho tam giác ABC có góc A nhọn, phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Gọi M là trung điểm của BC. Cm AM = 1/2 DE và AM vuông góc DE
a)Vẽ tam giác đề ABC. Ở phía ngoài tam giác ABC vẽ tam giác ABD vuông cân tại C.
b) Tính góc BDA
Hình vẽ:
\(\Leftrightarrow\widehat{BAD}=\widehat{BAC}+\widehat{CAD}=60^0+45^0=105^0\)
cho tam giac abc vẽ các tam giác abd;ace vuông cân tại d và e ở phía ngoài tam giác abc .M là trung diem của de: cm tam giác bnc vuong cân:






















