cho tam giác ABC các đường trung tuyến BD và CE vuông góc với nhau tại H . Biết AB = 5 cm ; AC = 6cm .tính cạnh BC.
c: Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hbh
=>M là trung điểm của HK
=>H,M,K thẳng hàng
d: BACK là hình thoi
=>M là trung điểm của AK và AK vuông góc BC
=>A,H,M thẳng hàng
=>ΔABC cân tại A
=>AB=AC
tham khảo
a.Ta có BK//CH(⊥AB),CK//BH(⊥AC)BK//CH(⊥AB),CK//BH(⊥AC)
→BHCK→BHCK là hình bình hành
b.Vì BHCKBHCK là hình bình hành
→HK∩BC→HK∩BC tại trung điểm mỗi đường
Do MM là trung điểm BCBC
→M→M là trung điểm HKHK
→H,M,K→H,M,K thẳng hàng
c.Ta có O,MO,M là trung điểm AK,HKAK,HK
→OM→OM là đường trung bình ΔAHKΔAHK
→OM//AH→OM//AH
Do BD∩CE=H→HBD∩CE=H→H là trực tâm ΔABC→AH⊥BCΔABC→AH⊥BC
→OM⊥BC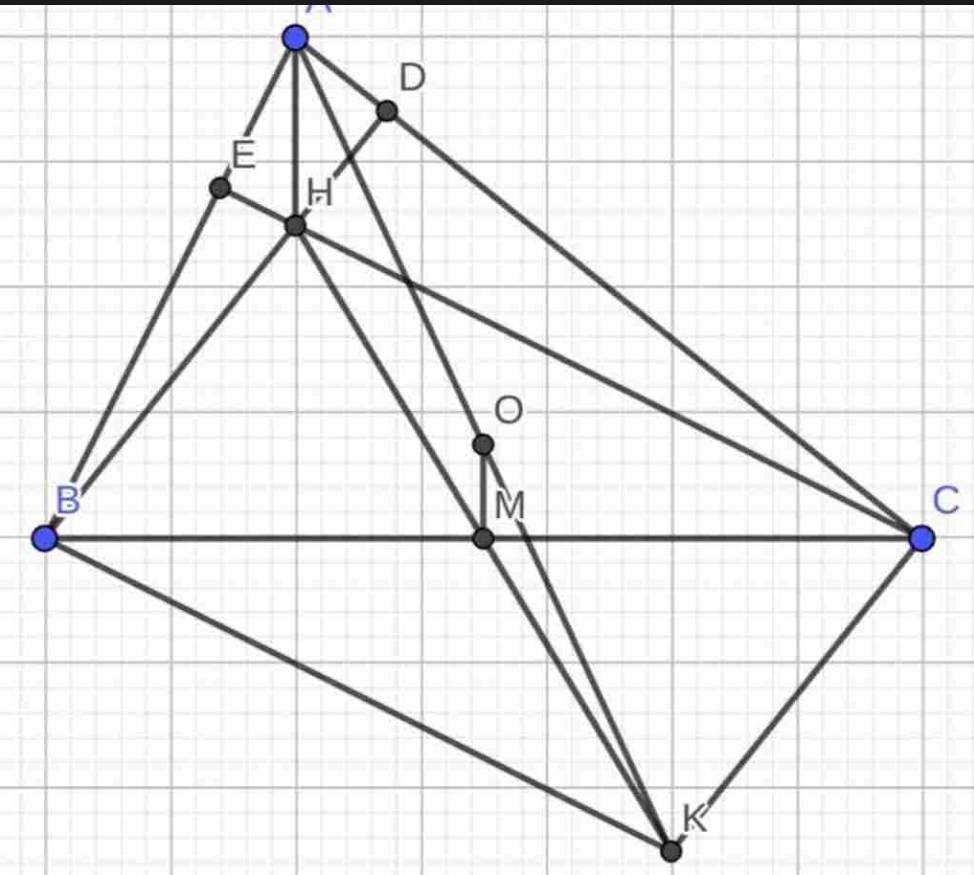
cho tam giác abc, các đường cao bd, ce cắt nhau tại h. đường vuông góc với ab tại b và đường vuông góc ac tại c cắt nhau ở k. gọi m là trung điểm của bc
a, cm tam giác adb đồng dạng tam giác aec
b, cm he.hc=hd.hb
c, cm h, k, m, thẳng hàng
d, tam giác abc phải có điều kiện gì thì tam giác bhck là hình thoi? hình chữ nhật?
a) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{EAC}\) chung
Do đó: ΔADB\(\sim\)ΔAEC(g-g)
Cho tam giác ABC, hai đường trung tuyến BD và CE vuông góc với nhau. Biết AB=5cm, AC=10cm.Vậy BC=?cm
Cho tam giác ABC có AB = 6 cm, AC = 8 cm. Hai đường trung tuyến BD và CE vuông góc với nhau tại I
Tính BC
Gọi G là giao điểm của BD và CE. Ta có G là trọng tâm của △ABC
Đặt GD=x,GE=y. Khi đó GB=2x,GC=2y.
Áp dụng định lý Pitago cho các tam giác vuông BGE, CGD, ta có:
GE2+GB2=BE2⇒y2+4x2=9 (1)
GD2+GC2=CD2⇒x2+4y2=16 (2)
Từ (1) và (2) ta có: 5(x2+y2)=25
⇒x2+y2=5
Áp dụng định lý Pitago cho tam giác vuông BGC, ta có:
BC2=GB2+GC2=4x2+4y2=20
Vậy: BC = \(\sqrt[2]{5}\)
Cho tam giác ABC có các đường trung tuyến BD và CF vuông góc với nhau Tính độ dài BC biết BD = 9 cm ,CE = 12 cm
Bài 1: Cho tam giác ABC có AB = 6 cm, AC = 8 cm. Hai đường trung tuyến BD và CE vuông góc với nhau tại G. Tính độ dài đoạn BC là?
Bài 2 : Cho tam giác ABC có hai đường phân giác BD và CE cắt nhau tại I. Chứng minh rằng : Nếu 2BI.CI = BD.CE thì tam giác ABC vuông ?
Bài 2: Goi G là giao điểm của 2 đường trung tuyến CE và BD ta có GD = 1/2 BG và EG = 1/2 CG [Vì theo tính chất của trung tuyến tại giao điểm G, của 3 đường ta có G chia đường trung tuyến ra làm 2 phần, phần này gấp đôi phần kia.]
Áp dụng định lý pythagore vào tam giác vuông BGE ta có:
BG^2 = EB^2 - EG^2 = 9 - EG^2 = 9 - (1/2. GC)^2 (1)
Áp dụng định lý pythagore vào tam giác vuông CGD ta có:
GC^2 = CD^2 - GD^2 = 16 - GD^2 = 16 - (1/2BG)^2 (2)
mặt khác BC^2 = BG^2 + GC^2. Do đó từ (1) và (2) ta có:
BC^2 = 9 -1/4 GC^2 + 16 - 1/4 BG^2 = 25 - 1/4(GC^2 + BG^2)
<=> BC^2 + 1/4(GC^2 + BG^2) = 25 <=> BC^2 + 1/4BC^2 = 25 <=> 5/4BC^2 = 25 <=>
BC^2 =25. 4/5 = BC^2 =20 <=> BC = căn 20 <=>
BC = 2.(căn 5) cm
Vì \(\Delta\)GDC vuông tại G nên theo định lý Py-ta-go ta có
\(DC^2=GD^2+GC^2\)(3)
Từ (1),(2) và (3) ta có
\(BC^2=EB^2-EG^2+DC^2-GD^2=\left(\frac{AB}{2}\right)^2-EG^2+\left(\frac{AC}{2}\right)^2-GD^2\)
\(\Rightarrow BC^2=\left(\frac{6}{2}\right)^2-EG^2+\left(\frac{8}{2}\right)^2-GD^2=3^2+4^2-\left(EG^2+GD^2\right)=25-\left(EG^2+GD^2\right)\)(4)
Mà ta có ED là đường trung bình của \(\Delta ABC\) nên ta có \(ED=\frac{BC}{2}\) (5)
Vì \(\Delta EDG\) vuông tại G nên áp dụng định lý Py-ta-go ta có
\(ED^2=GD^2+EG^2\) (6)
Từ (4),(5) và (6) ta có
\(BC^2=25-ED^2=25-\left(\frac{BC}{2}\right)^2=25-\frac{BC^2}{4}=\frac{100-BC^2}{\text{4}}\)
\(\Rightarrow\text{4BC^2}=100-BC^2\)
\(\Leftrightarrow5BC^2=100\)
\(\Leftrightarrow BC^2=20\)
\(\Leftrightarrow BC=\sqrt{20}\)(cm)
Vậy \(BC=\sqrt{20}cm\)
Cho tam giác ABC có hai đường trung tuyến BD và CE vuông góc với nhau. Biết rằng BD=9 cm,CE=12 cm.Tính BC
ta dựa theo định lí ba đường trung tuyến của một tam giác cùng đi qua 1 điểm. Điểm đó cách mỗi đỉnh bằng \(\frac{2}{3}\)độ dài đường trung tuyến.
9*2/3=6
12*2/3=8
vậy ta áp dụng định lí py ta go
AB^2+AC^2=BC^2
=> 6^2+8^2=100
căn của 100 là 10
Vậy BC=10
cho tam giác ABC cân tại A ( A < 90 độ ) . Kẻ BD vuông góc Ac ( D thuộc AC ) , CE vuông góc AB ( E thuộc AB ) , BD và CE cắt nhau tại H . a, CM : BD = CE . b, CM : tam giác BHC cân . c, CM : AH là đường trung trực của BC . d, TRên tia BD lấy điểm K sao cho D là trung điểm của BK . So sánh ECB và DKC
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc BAD chung
=>ΔADB=ΔAEC
=>BD=CE
b: góc ABD=góc ACE
=>góc HBC=góc HCB
=>ΔHBC cân tại H
c: AB=AC
HB=HC
=>AH là trung trực của BC
Cho tam giác ABC có AB = 6 cm AC = 8 cm hai đường trung tuyến BD và CE vuông góc với nhau tính BC
Goi G là giao điểm của 2 đường trung tuyến CE và BD ta có GD = 1/2 BG và EG = 1/2 CG [Vì theo tính chất của trung tuyến tại giao điểm G, của 3 đường ta có G chia đường trung tuyến ra làm 2 phần, phần này gấp đôi phần kia.]
Áp dụng định lý pythagore vào tam giác vuông BGE ta có:
BG^2 = EB^2 - EG^2 = 9 - EG^2 = 9 - (1/2. GC)^2 (1)
Áp dụng định lý pythagore vào tam giác vuông CGD ta có:
GC^2 = CD^2 - GD^2 = 16 - GD^2 = 16 - (1/2BG)^2 (2)
mặt khác BC^2 = BG^2 + GC^2. Do đó từ (1) và (2) ta có:
BC^2 = 9 -1/4 GC^2 + 16 - 1/4 BG^2 = 25 - 1/4(GC^2 + BG^2)
<=> BC^2 + 1/4(GC^2 + BG^2) = 25 <=> BC^2 + 1/4BC^2 = 25 <=> 5/4BC^2 = 25 <=>
BC^2 =25. 4/5 = BC^2 =20 <=> BC = căn 20 <=>
BC = 2.(căn 5) cm