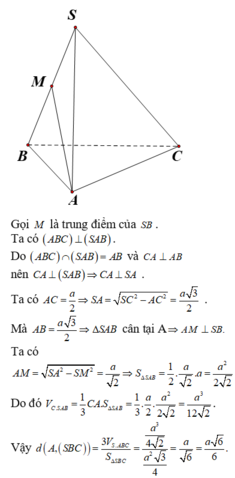
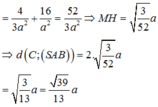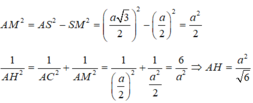Tam giác ABC vuông tại A có C^=300 ; AB = 12 cm thì BC = a. 12cm b. 6cm c. 24 cm d. Kết quả khác

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, có BC = a, AC = b, AB = c. Giải tam giác ABC, biết:
a, b = 5,4cm, C ^ = 30 0
b, c = 10cm, C ^ = 45 0
Cho tam giác ABC vuông tại A có AC 10cm,
C
^
30
0
. Tính AB, BC A. AB
5
3
3
; BC
20
3
3
B. AB
10
3...
Đọc tiếp
Cho tam giác ABC vuông tại A có AC = 10cm, C ^ = 30 0 . Tính AB, BC
A. AB = 5 3 3 ; BC = 20 3 3
B. AB = 10 3 3 ; BC = 14 3 3
C. AB = 10 3 3 ; BC = 20 3
D. AB = 10 3 3 ; BC = 20 3 3

Xét tam giác ABC vuông tại A có:

Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A,
A
B
C
^
30
0
. SBC là tam giác đều cạnh a và mặt bên SBC vuông góc với đáy. Khoảng cách từ điểm C đến mặt phẳng (SAB) là:
Đọc tiếp
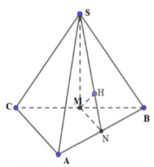
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, A B C ^ = 30 0 . SBC là tam giác đều cạnh a và mặt bên SBC vuông góc với đáy. Khoảng cách từ điểm C đến mặt phẳng (SAB) là:
![]()
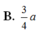
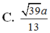
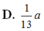
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A,
A
B
C
30
0
.
SBC là tam giác đều cạnh a và mặt bên SBC vuông góc với đáy. Khoảng cách từ điểm C đến mặt phẳng (SAB) là: A.
a
5
B.
3
a
4
C.
39
a...
Đọc tiếp
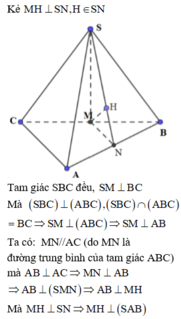
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, A B C = 30 0 . SBC là tam giác đều cạnh a và mặt bên SBC vuông góc với đáy. Khoảng cách từ điểm C đến mặt phẳng (SAB) là:
A. a 5
B. 3 a 4
C. 39 a 13
D. a 3
Chọn C.
Phương pháp:
Đưa về dựng khoảng cách từ M đến (SAB) với M là trung điểm của BC.
Cách giải:
Gọi M, N lần lượt là trung điểm của BC, AB.

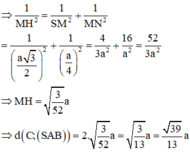
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có BC 5 cm, ∠C
30
0
. Trường hợp nào sau đây là đúng: A.
A
B
5
3
2
c
m
B. AB 2,5 cm C.
A
C
5
3
c
m
D.
A
C
5...
Đọc tiếp
Cho tam giác ABC vuông tại A có BC = 5 cm, ∠C = 30 0 . Trường hợp nào sau đây là đúng:
A. A B = 5 3 2 c m
B. AB = 2,5 cm
C. A C = 5 3 c m
D. A C = 5 3 3 c m
Đáp án là B
AB = BC.sin C = 5.sin 30 0 = 2,5 cm
Đúng 0
Bình luận (0)
Chọn câu đúng nhất.1 .Cho ∆ ABC vuông cân tại A. vậy góc B bằng:A. 600B. 900C. 450D. 12002. Một tam giác là vuông nếu độ dài 3 cạnh của nó là:A. 2,3,4 B. 3,4,5 C. 4,5,6 D. 6,7,83. Một tam giác cân có góc ở đáy là 350 thì góc ở đỉnh có số đo là:A. 1000B. 1100C. 850D. 12004. Tam giác ABC có BC 3cm ; AC 5cm ; AB 4cm. Tam giác ABC vuông tại đâu?A. Tại B B. Tại C C. Tại A D. Không phải là tam giác vuông5. Tam giác ABC có AB AC BC thì tam giác ABC là A. Tam giác nhọn B. Tam giác cân C. Tam giác v...
Đọc tiếp
Chọn câu đúng nhất.1 .Cho ∆ ABC vuông cân tại A. vậy góc B bằng:A. 600B. 900C. 450D. 12002. Một tam giác là vuông nếu độ dài 3 cạnh của nó là:A. 2,3,4 B. 3,4,5 C. 4,5,6 D. 6,7,83. Một tam giác cân có góc ở đáy là 350 thì góc ở đỉnh có số đo là:A. 1000B. 1100C. 850D. 12004. Tam giác ABC có BC = 3cm ; AC = 5cm ; AB = 4cm. Tam giác ABC vuông tại đâu?A. Tại B B. Tại C C. Tại A D. Không phải là tam giác vuông5. Tam giác ABC có AB = AC = BC thì tam giác ABC là A. Tam giác nhọn B. Tam giác cân C. Tam giác vuông D. Tam giác đều6. Tam giác nào vuông nếu độ lớn ba góc kà:A. 300, 700, 800B. 200, 700, 900 C. 650, 450, 700D. 600, 600, 6007. Tam giác cân là tam giác có:A. Hai cạnh bằng nhau -B. Ba cạnh bằng nhau - C. Một góc bằng 600 - D. Một góc bằng 900
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại A,
ABC
^
30
0
tam giác SBC đều cạnh a và mặt phẳng (SAB) vuông góc với mặt phẳng (ABC). Tính khoảng cách từ A đến (SBC). A.
a
6
B.
3
a
14
7
C. ...
Đọc tiếp
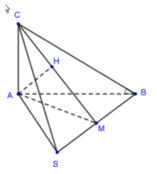
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại A, ABC ^ = 30 0 tam giác SBC đều cạnh a và mặt phẳng (SAB) vuông góc với mặt phẳng (ABC). Tính khoảng cách từ A đến (SBC).
A. a 6
B. 3 a 14 7
C. a 2 3
D. 2 a 7
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại A góc
A
B
C
^
30
0
; tam giác SBC là tam giác đều cạnh a và măt phẳng
S
A
B
⊥
mặt phẳng (ABC). Khoảng cách từ A đến mặt phẳng (SBC) là: A.
a
6...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại A góc A B C ^ = 30 0 ; tam giác SBC là tam giác đều cạnh a và măt phẳng S A B ⊥ mặt phẳng (ABC). Khoảng cách từ A đến mặt phẳng (SBC) là:
A. a 6 5
B. a 6 3
C. a 3 3
D. a 6 6