Hàm số nào trong các hàm số sau đồng biến trên khoảng ( 0 ; + ∞ )
A. y = lnx .
B. y = 2 - x
C. y = log 1 2 x
D. y = ( x - 1 ) - 3
Trong các hàm số sau hàm số nào là đồng biến trên khoảng (-π;0)
A. y = tanx
B. y = cotx
C. y = sinx
D. y = cosx
Hàm số nào trong bốn hàm số sau đồng biến trên khoảng 0 ; + ∞ ?
A. y = 1 − x 2
B. y = x ln x
C. y = e x − 1 x
D. y = x − π
Hàm số nào trong bốn hàm số sau đồng biến trên khoảng 0 ; + ∞ ?
A. y = 1 − x 2
B. y = x ln x
C. y = e x − 1 x
D. y = x − π
Đáp án C
Phương án A: y ' = − 2 x ⇒ y ' > 0, ∀ x ∈ − ∞ ; 0 và y ' < 0, ∀ x ∈ 0 ; + ∞ .
Khi đó hàm số y = 1 − x 2 đòng biến trên khoảng − ∞ ; 0 , nghịch biến trên khoảng 0 ; + ∞ .
Phương án B: y ' = ln x + 1 ⇒ y ' > 0, ∀ x ∈ 1 e ; + ∞ và y ' < 0, ∀ x ∈ 0 ; 1 e . Khi đó hàm số đồng biến trên 1 e ; + ∞ và nghịch biến trên 0 ; 1 e .
Phương án C: y ' = e x + 1 x 2 > 0, ∀ x ≠ 0 nên hàm số đồng biến trên mỗi khoảng − ∞ ; 0 và 0 ; + ∞ .
Phương án D: y ' = − π . x − π − 1 = − π x π + 1 ⇒ y ' < 0, ∀ x ∈ 0 ; + ∞ . Khi đó hàm số y = x − π nghịch biến trên khoảng 0 ; + ∞ .
Trong các hàm số sau, hàm số nào đồng biến trên khoảng - ∞ ; + ∞ ?
A. y = 2018 x
B. y = - 1 2 x 3 + x
C. y = log 5 1 x 2
D. y = log 3 x
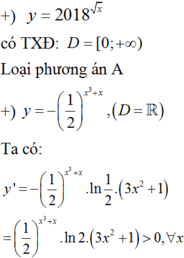
Hàm số nào đồng biến trên khoảng - ∞ ; + ∞
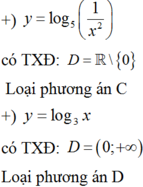
Chọn: B
Trong các hàm số sau, hàm số nào đồng biến trên khoảng 1 ; + ∞ ?
A. y = x − 4 x + 2 3
B. y = x − 2 2 x − 3
C. y = − x 3 + x − 1
D. y = 3 − x x + 1
Chọn A.
Phương pháp:
Tìm các khoảng đồng biến của mỗi hàm số ở các đáp án và đối chiếu kết quả.
Cách giải:

Nên hàm số ở đáp án A thỏa mãn.


Trong các hàm số sau, hàm số nào đồng biến trên khoảng 1 ; + ∞ ?
A. y = x 4 - x 2 + 3
B. y = x - 2 2 x - 3
C. y = - x 3 + x - 1
D. y = 3 - x x + 1
Trong các hàm số sau, hàm số nào chỉ đồng biến trên khoảng (-∞; 1) ?
A. y = 1 3 x 3 - 2 x 2 + 3 x - 1
B. y = - 2 x + 1 x - 1
C. y = x + 1 x 2 + 1
D. y = x - 1
Hàm số nào trong các hàm số sau đây đồng biến trên khoảng (1;3)?
A. y = 4 − x 2
B. y = x 4 − 2 x 2 − 1
C. y = e − x
D. y = x + 1 2 x − 3
Trong các hàm số sau, hàm số nào đồng biến trên khoảng − π 3 ; π 6 ?
A. y = tan 2 x + π 6
B. y = cot 2 x + π 6
C. y = sin 2 x + π 6
D. y = cos 2 x + π 6
Với x ∈ − π 3 ; π 6 → 2 x ∈ − 2 π 3 ; π 3 → 2 x + π 6 ∈ − π 2 ; π 2 thuộc góc phần tư thứ IV và thứ nhất nên hàm số y = sin 2 x + π 6 đồng biến trên khoảng − π 3 ; π 6 .
Chọn đáp án C.