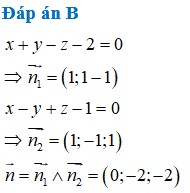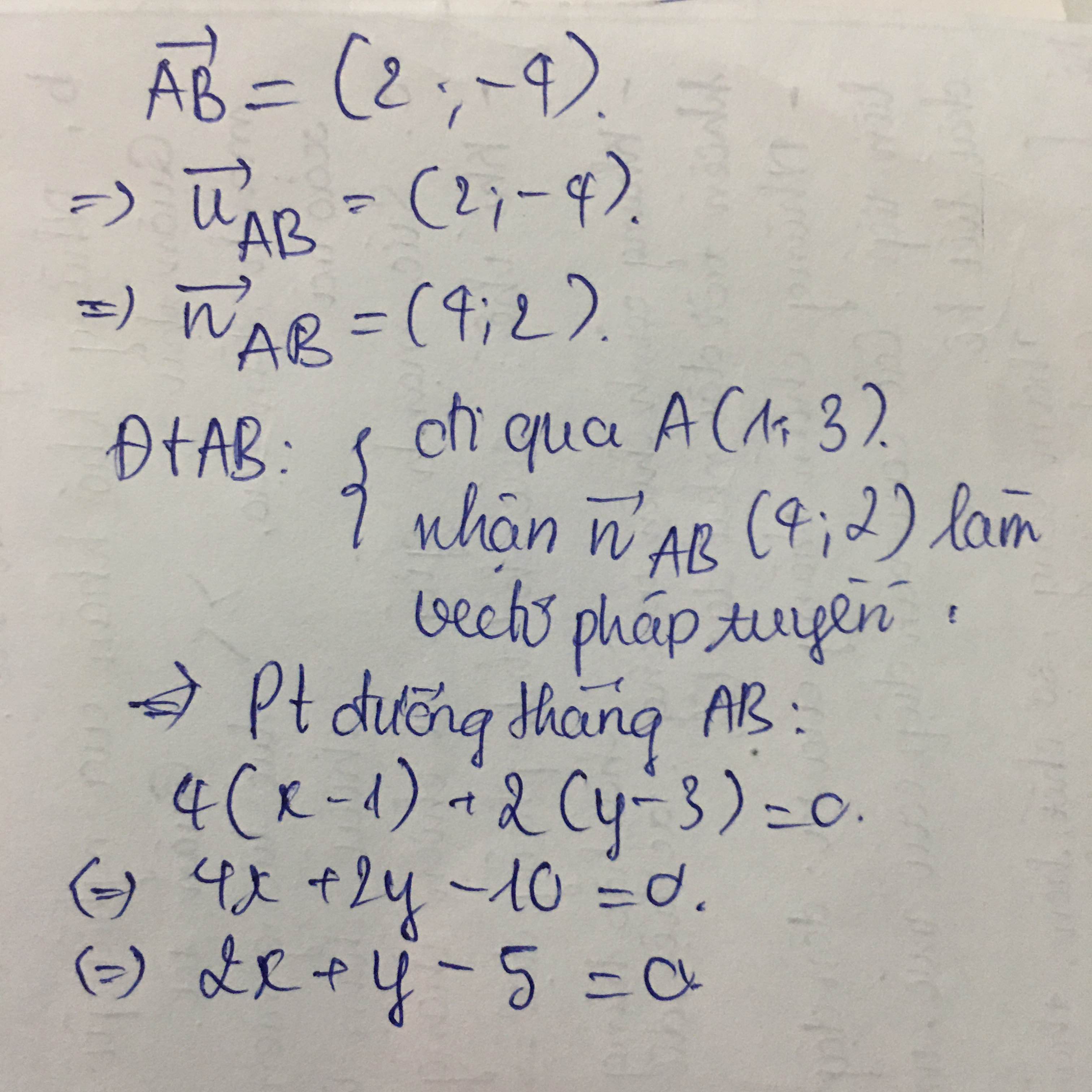Viết phương trình mặt phẳng (R) đi qua điểm A(1; 2; −1) và vuông góc với hai mặt phẳng (P): 4x – 2y + 6z – 11 = 0, (Q): 2x + 2y + 2z – 7 = 0.

Những câu hỏi liên quan
Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm
M
(
-
1
;
-
2
;
5
)
và vuông góc với hai mặt phẳng
(
Q
)
:
x
+
2
y
-
3
z
+
1
0
v
à
...
Đọc tiếp
Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M ( - 1 ; - 2 ; 5 ) và vuông góc với hai mặt phẳng ( Q ) : x + 2 y - 3 z + 1 = 0 v à ( R ) : 2 x - 3 y + z + 1 = 0 .
A. x- y + z – 6 = 0
B. x + y - z + 8 = 0
C. –x + y + z – 4 = 0
D. x + y + z - 2 = 0
Chọn D
![]()
![]()
![]()
nên mặt phẳng (P) nhận
![]()
và (P) đi qua điểm M(-1;-2;5) nên có phương trình là:
1 ( x + 1 ) + 1 ( y + 2 ) + 1 ( z - 5 ) = 0 h a y x + y + z - 2 = 0 .
Đúng 0
Bình luận (0)
Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm
M
(
-
1
;
-
2
;
5
)
và vuông góc với hai mặt phẳng
(
Q
)
:
x
+
2
y
-
3
z
+
1
0
v
à
(
R
)
:
2
x
-
3...
Đọc tiếp
Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M ( - 1 ; - 2 ; 5 ) và vuông góc với hai mặt phẳng ( Q ) : x + 2 y - 3 z + 1 = 0 v à ( R ) : 2 x - 3 y + z + 1 = 0 .
A. x- y + z – 6 = 0
B. x + y - z + 8 = 0
C. –x + y + z – 4 = 0
D. x + y + z - 2 = 0
Chọn D
![]()
![]()
![]()
nên mặt phẳng (P) nhận
![]()
và (P) đi qua điểm M(-1;-2;5) nên có phương trình là:
1 ( x + 1 ) + 1 ( y + 2 ) + 1 ( z - 5 ) = 0 h a y x + y + z - 2 = 0 .
Đúng 1
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm
A
(
3
;
0
;
0
)
,
B
(
0
;
–
4
;
0
)
,
C
(
0
;
0
;
4
)
.
Viết phương trình mặt phẳng (R) đi qua ba điểm A, B, C. A.
(
R
)
:
4...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A ( 3 ; 0 ; 0 ) , B ( 0 ; – 4 ; 0 ) , C ( 0 ; 0 ; 4 ) . Viết phương trình mặt phẳng (R) đi qua ba điểm A, B, C.
A. ( R ) : 4 x – 3 y + 3 z – 12 = 0
B. ( R ) : 4 x + 3 y + 3 z + 12 = 0
C. ( R ) : 3 x – 4 y + 4 z – 12 = 0
D. ( R ) : 3 x + 4 y + 4 z + 12 = 0 .
Đáp án là A
(R) là mặt phẳng có phương trình đoạn chắn là
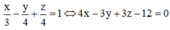
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(3;0;0), B(0;–4;0), C(0;0;4). Viết phương trình mặt phẳng (R) đi qua ba điểm A, B, C
A. (R) : 4x – 3y + 3z – 12 = 0
B. (R) : 4x + 3y + 3z + 12 = 0
B. (R) : 3x – 4y + 4z – 12 = 0
D. (R) : 3x + 4y + 4z + 12 = 0
Viết phương trình mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng x+y-z-2=0, x-y+z-1=0
A. x+y+z-3=0
B. y+z-2=0
C. x+z-2=0
D. x-2y+z=0
Viết phương trình mặt phẳng (P) đi qua ba điểm A(-3;0;0), B(0;-2;0), C(0;0;-1). A.
2
x
+
3
y
+
6
z
+
6
0
B.
2
x
-
3
y
+
6
z
+
6
0
C.
x
3
+...
Đọc tiếp
Viết phương trình mặt phẳng (P) đi qua ba điểm A(-3;0;0), B(0;-2;0), C(0;0;-1).
A. 2 x + 3 y + 6 z + 6 = 0
B. 2 x - 3 y + 6 z + 6 = 0
C. x 3 + y 2 + z 1 = 1
D. x 3 + y 2 + z 1 = 0
Trong mặt phẳng Oxy, cho ba điểm A(1;3); B(3;-1) và C(-2; 3).
a. Viết phương trình qua hai điểm A, B.
b. Viết phương trình đường thẳng d đi qua C, đồng thơi d cách đều A và B.
Viết phương trình mặt phẳng (P) đi qua điểm A (0; -1; 2), song song với trục Ox và vuông góc với mặt phẳng (Q) : x + 2y - 2z +1 0. A. (P) : 2y + 2z - 1 0 B. (P) : y + z - 1 0 C. (P) : y - z + 3 0 D. (P) : 2x + z - 2 0
Đọc tiếp
Viết phương trình mặt phẳng (P) đi qua điểm A (0; -1; 2), song song với trục Ox và vuông góc với mặt phẳng (Q) : x + 2y - 2z +1 = 0.
A. (P) : 2y + 2z - 1 = 0
B. (P) : y + z - 1 = 0
C. (P) : y - z + 3 = 0
D. (P) : 2x + z - 2 = 0
Viết phương trình mặt phẳng (P) đi qua điểm A(0; -1; 2), song song với trục Ox và vuông góc với mặt phẳng (Q) : x + 2y - 2z +1 0.
Đọc tiếp
Viết phương trình mặt phẳng (P) đi qua điểm A(0; -1; 2), song song với trục Ox và vuông góc với mặt phẳng (Q) : x + 2y - 2z +1 = 0.
![]()
![]()
![]()
![]()
Trong không gian tọa độ Oxyz cho điểm
A
1
;
2
;
3
và hai mặt phẳng
P
:
x
−
y
0
,
Q
:
2
x
+
4
z
+
1
0
. Phương trình mặt phẳng (R) đi qua A và chứa giao tuyến của hai mặt phẳng (P),(Q) là A....
Đọc tiếp
Trong không gian tọa độ Oxyz cho điểm A 1 ; 2 ; 3 và hai mặt phẳng P : x − y = 0 , Q : 2 x + 4 z + 1 = 0 . Phương trình mặt phẳng (R) đi qua A và chứa giao tuyến của hai mặt phẳng (P),(Q) là
A. R : − 2 x + 2 y − z + 3 = 0.
B. R : 2 x − 2 y − z + 3 = 0.
C. R : 2 x + 2 y + 3 z − 17 = 0.
D. R : x - y + 1 = 0.
Đáp án D
Gọi d = P ∩ Q ,d có VTCP là u → .
Khi đó u → = 1 ; − 1 ; 0 , 2 ; 0 ; 4 = − 4 ; − 4 ; 2 = − 2 2 ; 2 ; − 1 .
Mặt phẳng (R) qua A 1 ; 2 ; 3 , có VTCP là 2 ; 2 ; − 1 và đi qua điểm B ( − 1 2 ; − 1 2 ; 0 ) thuộc giao tuyến, (R) có phương trình là R : x − y + 1 = 0.
Đúng 0
Bình luận (0)