Cho hình thang ABCD. Hai đường chéo AC và BD cắt nhau tại I. Tìm các cặp tam giác có diện tích bằng nhau
Những câu hỏi liên quan
Cho hình thang ABCD. Hai đường chéo AC và BD cắt nhau tại I. Tìm các cặp tam giác có diện tích bằng nhau.
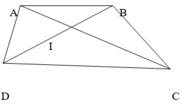
Ta có 3 cap tam giác có diện tích bằng nhau là
S ADB = SABC (vì cùng đáy AB x chiều cao chia 2)
SACD = SBCD
SAID = SIBC
Vì chúng đều là phần diện tích còn lại của 2 tam giác có diện tích bằng nhau và có chung 1 phần diện tích. (Tam giác ICD hoặc AIB)
Đúng 0
Bình luận (0)
cho hình thang ABCD có hai đường chéo AC và BD cắt nhau tại I .tìm các cặp tam giác có diện tích bằng nhau
dien dien . khong du thong tin lam sao ma lam duoc . nam moi to li xi cau chu ngu
Đúng 0
Bình luận (0)
Cho hình thang ABCD. Hai đường chéo AC và BD cắt nhau tại I. Tìm các cặp tam giác có diện tích bằng nhau.
cho hình thang ABCD. Kẻ hai đường chéo AC và BD , chúng cắt nhau tại I . Hãy tìm các cặp tam giác có diện tích bằng nhau trong các hình thang đã cho
Cho hình thang ABCD Hai đường chéo AC và BD cắt nhau tại I. Tìm các cặp tam giác có diện tích băng nhau
Cho hình thang ABCD . Hai đường chéo AC và BD cắt nhau tại E . Tìm các cặp hình tam giác có diện tích bằng nhau . ( giải thích )
Kẻ AH vuông góc vs DC và BE tương tự như vậy
=> AH = BE
Ta có diện tích tam giác ADC=1/2AH x DC
diện tích tam giác BDC=1/2BE x DC
mà AH=BE
=> S ADC = S BDC
Đây chỉ là 1 căp thôi tck mik đi mik làm tiếp cho
Đúng 0
Bình luận (0)
Bạn tìm các cặp tam giác chung đáy và chung đỉnh là xong
Đúng 0
Bình luận (0)
Cho hình thang ABCD . Hai đường chéo AC và BD cắt nhau tại I . Hãy tìm các cặp tam giác có diện tích bằng nhau,
các bạn giải giúp mình nhé !!!!
Cho hình thang ABCD có đáy bé AB = \(\dfrac{1}{3}\)CD. Hai đường chéo AC và BD cắt nhau tại O. a) Tìm các cặp tam giác có diện tích bằng nhau. b) Biết diện tích tam giác ABC là 24cm2. Tính diện tích hình thang ABCD.
Cho hình thang ABCD . Hai đường chéo AC và BD cắt nhau tại I . Xác định các cặp tam giác có diện tích bằng nhau ( có giải thích và vẽ hình )
Kẻ đường cao AH, BK, vì AB//HK mà AHK=HKB=90 nên AHKB là hình chữ nhật
\(\Rightarrow\)AH=BK; \(\Delta ADC\)và\(\Delta BDC\)có chung đáy, 2 đường cao bằng nhau nên diện tích bằng nhau
Bằng cách tương tự ta chứng minh được \(S_{DAB}=S_{CAB}\)
Đúng 0
Bình luận (0)