cho tam giác abc cân tại a có góc a 20 độ tren AB lay M sao cho AM=BC Tinh goc BMC

Những câu hỏi liên quan
cho tam giac ABC can tai A co goc A=20 da ve tam giac BMC deu sao cho M va A nam tren cung 1 nua mp bo BC tren AB lay D sao cho AD =BC a,CM AM la tia phan giac cua BAC b, tinh goc ACD
cho tam giác abc có goc A nhọn, tren nủa mat phang bo ab khong chua c lay diem N sao cho Na=AB và góc NAB =90 độ . tren mua mat phang bo AC khong chua B lay diem M sao cho MA = CA và góc MAC=90 độ . qua A kẻ đường thẳng vuong goc BC cắt MN tại K. cmK la trung diem cua MN
Cho tam giác ABC cân tại A có góc B bằng góc C =40 độ. Kẻ tia phân giác BD. Trên tia AB lấy điểm M sao cho AM=BC.
a) CM: BD+AD=BC
b) Tinh goc AMC ?
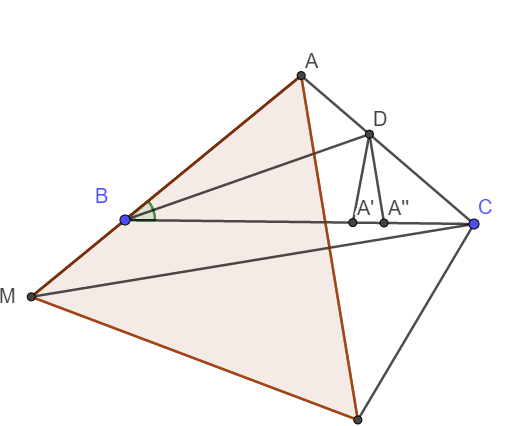
a) Trên BC lấy điểm A' và A'' sao cho BA' = BA; BA'' = BD
Do BD là phân giác góc ABA' nên ta có ngay \(\Delta ABD=\Delta A'BD\left(c-g-c\right)\)
\(\Rightarrow AD=A'D\) ; \(\widehat{BA'D}=\widehat{BAD}=180^o-40^o.2=100^o\)
\(\Rightarrow\widehat{DA'A''}=80^o\)
Xét tam giác cân BDA'' có: \(\widehat{DBA''}=20^o\Rightarrow\widehat{BA''D}=\frac{180^o-20^o}{2}=80^o\)
Suy ra DA' = DA'' và \(\widehat{A''DC}=\widehat{DA''A'}-\widehat{ACB}=40^o\)
Nên DA'' = CA''
Tóm lại thì AD = DA' = DA'' = A''C nên BC = BA''+ A''C = BD + AD
b) Vẽ tam giác đều AMF.
Ta có ngay \(\widehat{MAF}=60^o\Rightarrow\widehat{CAF}=100^o-60^o=40^o\)
Suy ra \(\Delta ABC=\Delta CAF\left(c-g-c\right)\)
\(\Rightarrow AC=CF\)
Từ đó ta có \(\Delta AMC=\Delta FMC\left(c-c-c\right)\)
\(\Rightarrow\widehat{AMC}=\widehat{FMC}\) hay MA là phân giác óc AMF.
Vậy nên \(\widehat{MAC}=30^o\)
Đúng 1
Bình luận (0)
cho tam giac ABC vong goc tai A co AB=6 cm,AC=8cm,BC=10 cm.Tren canh AB lay diem M sao cho AM= 4cm,tren canh BC lay diem N sao cho AN=2 cm,tren canh BC lay diem E sao cho BE=5 cm.Tinh:
a)chu ci va dien tich tam giac ABC.
b)diện tích tam giác MNE.
Sai đề thì phải N thuộc AC mới đúng.
a. Chu vi tam giác ABC = 6+8+10=24cm
Diện tích tam giác ABC =1/2.6.8 = 24 cm2
b.
từ E kể EK vuông góc AC tại K
Diện tích tam giác MNE = diện tích hình thang vuông MAKE - diện tích 2 tam giác AMN và NKE
EK//AB, E trung điểm BC => EK=1/2AB = 3cm, K là trung điểm AC=> AK=4cm =>NK=AN=2cm
Diện tích H.thang MAKE = 1/2.(3+4).4=14 cm2
Diện tích tam giac AMN = 1/2.2.4 = 4 cm2 và dt tam giác NKE=1/2.2.3 = 3cm2
=>dt tam giac MNE = 14-4-3= 7 cm2
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, có góc A = 20 độ. Trên cạnh AB lấy điểm M sao cho AM=BC. Tính góc AMC
Vẽ tam giác đều ACD sao cho d thuộc nmp bờ AC không chứa M
Có
góc A=200
\(\Rightarrow\)góc DAM=800
nên góc ADM=200
Dễ cm được tam giác ABC=tam giác DAM(c.g.c)
nên góc C=góc DMA
có góc ADC-góc ADM=góc MDC
nên góc MDC=400
nên góc DMC=700
Vậy góc AMC=700+DMA=1500
Đúng 0
Bình luận (0)
bạn Cam Hai Dang viết lòi giải rõ hơn dc ko kkkkk.
Cho tam giác cân tại A, có góc A bằng 90 độ. Trên cạnh AB lấy điểm M sao cho AM=BC. Từ M kẻ tia Mx//BC( Mx thuộc cùng nửa mp bờ AB chứa điểm C). Trên tia Mx lấy điểm E sao cho ME=AC
a, Cm tam giácEMA =tam giác ABC
b, Tính góc BMC
cho tam giác ABC vuông tại A . vẽ tia phân giác BD của góc ABC (D thuộc AC).Trên BC lấy E sao cho AB = EB.a, CMR tam giác ABD=tam giácEBD và ED vuông góc với BC
b,kẻ tia phân giác CM của góc ACB (m thuộc AB) cắt BD tại I .tinh goc BIC
c,tren BC lay N sao cho AC=NC AN cat BD tai o. Chứng minh tam giác AOE là tam giác vuông
cho tam giác abc cân tại a goc a 45 do tu trung diem I cua AC ve duong thang vuong goc voi Ac cat BC o M tren tia doi AM lay N sao cho AN=BM chung minh a, goc AMC=goc BAC b, tam giac ABM= tam giac CAN c, tam giac MNC vuong can tai C
Cho tam giác abc cân tại A có góc A = 30 độ đường cao AH trên cạnh AH lấy điểm M sao cho AM=BC chứng minh rằng tam giác BMC là tam giác đều













