A, DỄ DÀNG NHẬN THẤY AF VÀ BE LÀ CÁC TIA PHÂN GIÁC ( DO TAM GIÁC ABC ĐỀU)

=> CO LÀ TIA PHÂN GIÁC CỦA GÓC ACB

=> ACO = 30

DỄ DÀNG TÍNH ĐƯỢC OBC = 30

=> OBC = ACO

DO TAM GIÁC ABC ĐỀU => O LÀ GIAO ĐIỂM CỦA 3 ĐƯỜNG TRUNG TRỰC

=> OB = OC

TỪ ĐÓ DỄ DÀNG CHỨNG MINH ĐƯỢC TAM GIÁC OBM = TAM GIÁC OCN ( C.G.C)

=> OM = ON

B,  KẺ FH VUÔNG GÓC VỚI EF, NQ VUÔNG GÓC VỚI EF

DO CF = AE , CN = BM

=> MF = NE

LẠI CÓ GÓC NEQ = CEF = CFE = 60

=> NEQ = CFE

TỪ ĐÓ DỄ DÀNG CHỨNG MINH ĐƯỢC TAM GIÁC NQE = TAM GIÁC MHF ( G.C.G)

=> NQ = MH

TA CÓ NE SONG SONG VỚI MH , NQ = MH

=> MQNH LÀ HÌNH BÌNH HÀNH

=> QH CẮT MN TẠI TRUNG ĐIỂM CỦA MN

MÀ I LÀ TRUNG ĐIỂM CỦA MN

=> I THUỘC HQ

=> I THUỘC EF

=> ĐPCM

C, BÀI NÀY TỰ VẼ HÌNH NHÉ

TỪ M,N KỂ ĐƯỜNG VUÔNG GÓC VỚI AB CẮT AB TẠI H VÀ K. TỪ M KỂ ĐƯỜNG VUÔNG GÓC VỚI NK CẮT NK TẠI Q

=> MN LỚN HƠN HOẶC BẰNG MQ

MÀ MQ =HK

=> MN LỚN HƠN HOẶC BẰNG HK

MẶT KHÁC KA + HB = 1/2 AN + 1/2 BM = 1/2 AB = 1/2 BC = 1/2 AC

=> HK = 1/2 AB

=> MN LỚN HƠN HOẶC BẰNG 1/2AB

DẤU BẰNG XẢY RA KHI VÀ CHỈ KHI M VÀ N LÀ TRUNG ĐIỂM CỦA AC VÀ BC

( MÌNH MỚI HỌC LỚP 7)

Nhac cau 3

Tu M,N ke duong vuong goc voi AB cat AB tai H va K.Tu M ke duong vuong goc voi NK cat NK tai Q

=>MN\(_{\ge}\)MQ. Ma MQ=HK

=>MN\(\ge\)HK

Mat \(\ne\)KA+HB=1/2AN+1/2BM=1/2AB=1/2BC=1/2CA

=>HK=1/2AB

=>MN\(\ge\)1/2AB.dau bang xay ra khi M,N la trung diem cua cac canh

xin lỗi chị, em mới học lớp 5 thôi nên ko biết, mong chị tha lỗi. Chúc chị học giỏi nha

a.xét tam giác BAN và tam giác CAM ta có:
AM=AN (GT)
AB=AC ( tam giác ABC cân tại A)
A là góc chung
suy ra tam giác BÀN= tam giác CẤM (c.g.c)

b. xét tam giác OBM và tam giác OCN ta có:
góc OBM=góc OCN (2 góc tương ứng)
BM=CN (AB=AC mà AM=AN)
Góc OMB= góc ONC (góc ANB= góc AMC mà AMC+OMB=ANB+ONC)
suy ra tam giác OMB= ta giác ONC (g.c.g)

c.xét tam giác AMO và tam giác ANO ta có:
AM=AN(GT)
góc AMO= góc ANO ( tam giác AMC= tam giác ANB)
OM=ON (tam giác MOB= tam giác NOC)
suy ra tam giác AMO=tam giác ANO (c.g.c)
suy ra góc BAO= góc CAO (2 góc tương ứng). suy ra Ao là p/g của góc A

gọi giao điểm của BC và AO là I.
Xét tam giác ABI và tam giác ACI ta có:
AB=AC (tam giác ABC cân tại A)
góc BAI= góc CAI (CMT)
AI là cạnh chung
suy ra tam giác ABI= tam giác ACI( c.g.c)
suy ra góc AIB= góc AIC (2 góc tương ứng) mà AIB+AIC= 180 độ nên AIB=AIC=180/2=90 độ suy ra AI vuông góc vs Bc. suy ra AO là đường cao của tam giác ABC.

d. khi M,N lần lượt là trung điểm của AB và AC thì BM=MN=NC.

a.xét tam giác BAN và tam giác CAM ta có:
AM=AN (GT)
AB=AC ( tam giác ABC cân tại A)
A là góc chung
suy ra tam giác BÀN= tam giác CẤM (c.g.c)

b. xét tam giác OBM và tam giác OCN ta có:
góc OBM=góc OCN (2 góc tương ứng)
BM=CN (AB=AC mà AM=AN)
Góc OMB= góc ONC (góc ANB= góc AMC mà AMC+OMB=ANB+ONC)
suy ra tam giác OMB= ta giác ONC (g.c.g)

c.xét tam giác AMO và tam giác ANO ta có:
AM=AN(GT)
góc AMO= góc ANO ( tam giác AMC= tam giác ANB)
OM=ON (tam giác MOB= tam giác NOC)
suy ra tam giác AMO=tam giác ANO (c.g.c)
suy ra góc BAO= góc CAO (2 góc tương ứng). suy ra Ao là p/g của góc A

gọi giao điểm của BC và AO là I.
Xét tam giác ABI và tam giác ACI ta có:
AB=AC (tam giác ABC cân tại A)
góc BAI= góc CAI (CMT)
AI là cạnh chung
suy ra tam giác ABI= tam giác ACI( c.g.c)
suy ra góc AIB= góc AIC (2 góc tương ứng) mà AIB+AIC= 180 độ nên AIB=AIC=180/2=90 độ suy ra AI vuông góc vs Bc. suy ra AO là đường cao của tam giác ABC.

d. khi M,N lần lượt là trung điểm của AB và AC thì BM=MN=NC.

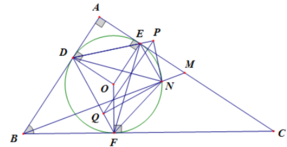
Vì DPN+DQN=90^o+90^o=180^o nên DPNQ là tứ giác nội tiếp

=>QPN=QDN (hai góc nội tiếp cùng chắn cung QN) (5)

Mặt khác DENF là tứ giác nội tiếp nên QDN=FEN  (6)

Từ (5) và (6) ta có FEN=QPN (7)

Tương tự ta có: EFN=PQN  (8)

Từ (7) và (8) suy ra  Δ N P Q ~ Δ N E F ( g . g ) = > P Q E F = N Q N F

Theo quan hệ đường vuông góc – đường xiên, ta có

N Q ≤ N F = > P Q E F = N Q N F ≤ 1 = > P Q ≤ E F

Dấu bằng xảy ra khi Q ≡ F ⇔ NF ⊥ DF ⇔ D, O, N thẳng hàng.

Do đó PQ max khi M là giao điểm của AC và BN, với N là điểm đối xứng với D qua O.