Cho tam giác ABC, đường cao AH. Lấy M, N thuộc BC, Q thuộc AB, P thuộc AC sao cho MNPQ là HCN. Tìm vị trí của P, Q sao cho diện tích MNPQ lớn nhất

Những câu hỏi liên quan
Cho tam giác ABC vuông cân tại A. BC = 36cm. Vẽ hình chữ nhật MNPQ có M thuộc AB; Q thuộc AC; P,N thuộc BC . Xác định vị trí của MN để diện tích MNPQ lớn nhất
Cho tam giác ABC vuông cân tại A. BC = 36cm. Vẽ hình chữ nhật MNPQ có M thuộc AB; Q thuộc AC; P,N thuộc BC . Xác định vị trí của MN để diện tích MNPQ lớn nhất
Cho tam giác ABC có BC 16cm , đường cao AH 12 cm. Một hình chữ nhật MNPQ có đỉnh M thuộc cạnh AB, đỉnh N thuộc cạnh AC còn hai đỉnh P và Q thuộc cạnh BC (h.17). Xác định vị trí của điểm M trên cạnh AB sao cho diện tích của hình chữ nhật đó bằng
36
c
m
2
.Hình 17
Đọc tiếp
Cho tam giác ABC có BC = 16cm , đường cao AH = 12 cm. Một hình chữ nhật MNPQ có đỉnh M thuộc cạnh AB, đỉnh N thuộc cạnh AC còn hai đỉnh P và Q thuộc cạnh BC (h.17). Xác định vị trí của điểm M trên cạnh AB sao cho diện tích của hình chữ nhật đó bằng 36 c m 2 .
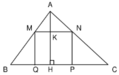
Hình 17
Vì ∆ ABC đồng dạng với ∆ AMN nên:
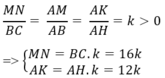
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
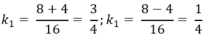
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
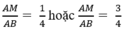
Đúng 0
Bình luận (0)
Cho tam giác ABC có BC 16cm , đường cao AH 12 cm. Một hình chữ nhật MNPQ có đỉnh M thuộc cạnh AB, đỉnh N thuộc cạnh AC còn hai đỉnh P và Q thuộc cạnh BC (h.17). Xác định vị trí của điểm M trên cạnh AB sao cho diện tích của hình chữ nhật đó bằng 36cm2.Hình 17
Đọc tiếp
Cho tam giác ABC có BC = 16cm , đường cao AH = 12 cm. Một hình chữ nhật MNPQ có đỉnh M thuộc cạnh AB, đỉnh N thuộc cạnh AC còn hai đỉnh P và Q thuộc cạnh BC (h.17). Xác định vị trí của điểm M trên cạnh AB sao cho diện tích của hình chữ nhật đó bằng 36cm2.
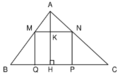
Hình 17
Vì ∆ ABC đồng dạng với ∆ AMN nên:
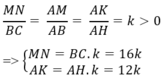
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
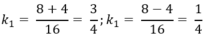
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
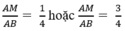
Đúng 0
Bình luận (0)
CHO TAM GIÁC ABC CÓ 3 GÓC NHỌN, AH LÀ ĐƯỜNG CAO VÀ AH=BC. MNPQ LÀ HÌNH CHỮ NHẬT NỘI TIẾP TAM GIÁC ABC (M, N THUỘC CẠNH BC, P THUỘC AC, Q THUỘC AB). TÌM CÁCH DỰNG ĐỂ SMNPQ LỚN NHẤT VÀ CHU VI MNPQ KHÔNG ĐỔI
cho tam giác ABC, góc ABC=60 độ. BC=a,AC=c. Hình chư nhật MNPQ có M thuộc AB, N thuộc AC, P,Q thuộc BC. Tìm M thuộc AB để diện tích MNPQ lớn nhất.
cho tam giác ABC, góc ABC=60 độ. BC=a,AC=c. Hình chư nhật MNPQ có M thuộc AB, N thuộc AC, P,Q thuộc BC. Tìm M thuộc AB để diện tích MNPQ lớn nhất.

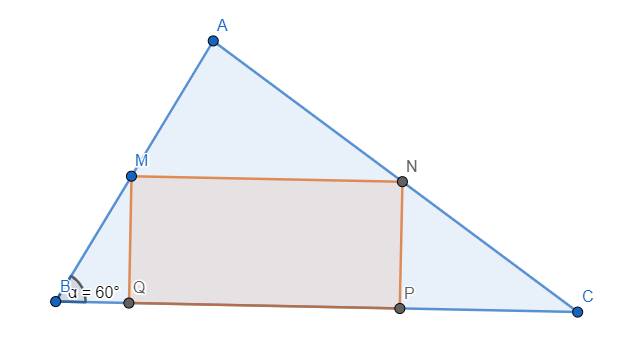
Đặt \(MB=m>0\). \(\Rightarrow MQ=NP=\dfrac{m}{\sqrt{3}}\)
Đặt \(AB=b>m\). Khi đó \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)
\(\Rightarrow MN=\dfrac{AM.BC}{AB}=\dfrac{\left(b-m\right).a}{b}=\left(1-\dfrac{m}{b}\right).a\) \(=a-\dfrac{a}{b}.m\)
\(\Rightarrow S_{MNPQ}=MN.NP=\dfrac{1}{\sqrt{3}}m\left(a-\dfrac{a}{b}.m\right)\)
\(=\dfrac{a}{b\sqrt{3}}\left(-m^2+bm\right)\)
\(=\dfrac{a}{b\sqrt{3}}\left(-m^2+2m.\dfrac{b}{2}-\dfrac{b^2}{4}+\dfrac{b^2}{4}\right)\)
\(=\dfrac{a}{b\sqrt{3}}\left[-\left(m-\dfrac{b}{2}\right)^2+\dfrac{b^2}{4}\right]\)
\(=-\dfrac{a}{\sqrt{3}}\left(m-\dfrac{b}{2}\right)^2+\dfrac{ab}{4\sqrt{3}}\) \(\le\dfrac{ab}{4\sqrt{3}}\), suy ra \(S_{MNPQ}\le\dfrac{ab}{4\sqrt{3}}\)
Dấu "=" xảy ra \(\Leftrightarrow m=\dfrac{b}{2}\) hay M là trung điểm của đoạn AB.
Vậy để diện tích hình chữ nhật MNPQ lớn nhất khi và chỉ khi M là trung điểm AB.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A có BC = 36 cm. Vẽ hình chữ nhật MNPQ sao cho M thuộc AB ; N , P thuộc BC ; Q thuộc AC
tính diện tích lớn nhất của hình chữ nhật MNPQ
Trl :
-Câu này có trong Vio Toán tv lớp 8 ( tớ vừa mới thi ạ :33 )
-Hơi ngại làm :> Nhưng cho cậu kq nhé : 162 cm2
100%
1/ Cho hình vuông ABCD. Lấy M tùy ý trên cạnh BC. Đường thẳng vuông góc AM tại M, cắt CD tại N. Tìm vị trí của M để CN lớn nhất2/ Cho hình vuông ABCD. Lấy M,N,P,Q thuộc 4 cạnh AB,BC,CD,AD. TÌm điều kiện của tứ giác MNPQ để chu vi tứ giác MNPQ nhỏ nhất3/ Lấy I nằm trong tam giác ABC nhọn. Vẽ IH⊥BC,IK⊥AC,IL⊥AB. Xác định vị trí của I để AL^2+BH^2+CK^2 nhỏ nhất4/ Cho tam giác ABC nhọn. Tìm điểm M trong tam giác sao cho AM.BC+BM.AC+CM.AB nhỏ nhất
Đọc tiếp
1/ Cho hình vuông ABCD. Lấy M tùy ý trên cạnh BC. Đường thẳng vuông góc AM tại M, cắt CD tại N. Tìm vị trí của M để CN lớn nhất
2/ Cho hình vuông ABCD. Lấy M,N,P,Q thuộc 4 cạnh AB,BC,CD,AD. TÌm điều kiện của tứ giác MNPQ để chu vi tứ giác MNPQ nhỏ nhất
3/ Lấy I nằm trong tam giác ABC nhọn. Vẽ \(IH⊥BC,IK⊥AC,IL⊥AB\). Xác định vị trí của I để \(AL^2+BH^2+CK^2\) nhỏ nhất
4/ Cho tam giác ABC nhọn. Tìm điểm M trong tam giác sao cho AM.BC+BM.AC+CM.AB nhỏ nhất












