cho tứ giác ABCD Chứng minh rằng :
a) Nếu AC=AD thì BC<BD
b) Nếu chu vi tam giác ABD không lớn hơn chu vi tam giác ACD thì AB<AC
Cho hình thang ABCD có AB // CD. Chứng minh rằng: Nếu AD+AC=BC+BD thì tứ giác ABCD là hình thang cân
cho tứ giác ABCD. Chứng minh rằng:
a) Nếu AC=AD thì BC<BD
b)Nếu chu vi tam giác ADB không lớn hơn chu vi tam giác ACD thì AB<AC
Cho tứ giác ABCD. Chứng minh rằng nếu |vecto AD + vecto BC| = |vecto AB + vecto DC| thì AC vuông góc với BD
Cho hình thang ABCD (AB//CD). Chứng minh rằng nếu AD+AC=BC+BD thì tứ giác ABCD là hình thang cân. Giúp mình gấp với.
Bài 1 cho tứ giác ABCD, P,Q lần lượt là trung điểm của AD và BC,a chứng minh PQ hoặc AB AC 2,b tứ giác ABCD là hình thang PQ AB CD 2. Bài 2 cho hình thang ABCD, AB đáy lớn. M ,N,P,Q lần lượt là trung điểm của AD BC AC BD.a chứng Minh M N P Q thẳng hàng.b Cho AB a CD b với a b. Tính MN PQ.c Cm rằng nếu MP PQ QN thì a 2b
Chứng minh rằng nếu tứ diện ABCD có AB ⊥ CD và AC ⊥ BD thì AD ⊥ BC.
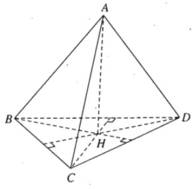
Vẽ AH ⊥ (BCD) tại H, ta có CD ⊥ AH và vì CD ⊥ AB ta suy ra CD ⊥ BH. Tương tự vì BD ⊥ AC ta suy ra BD ⊥ CH
Vậy H là trực tâm của tam giác BCD tức là DH ⊥ BC
Vì AH ⊥ BC nên ta suy ra BC ⊥ AD
Cách khác: Trước hết ta hãy chứng minh hệ thức:
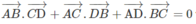
với bốn điểm A, B, C, D bất kì.
Thực vậy , ta có:
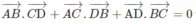
Do đó nếu AB ⊥ CD nghĩa là
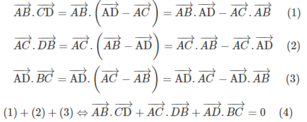
Từ hệ thức (4) ta suy ra
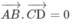 ,
,
do đó AD ⊥ BC.
Bài 1 cho tứ giác ABCD, P,Q lần lượt là trung điểm của AD và BC,
a) chứng minh PQ< hoặc = AB+AC/2,
b) tứ giác ABCD là hình thang <=> PQ=AB+CD/2.
Bài 2: cho hình thang ABCD, AB đáy lớn. M ,N,P,Q lần lượt là trung điểm của AD BC AC BD.
a) chứng Minh M N P Q thẳng hàng.
b) Cho AB=a CD=b với a>b. Tính MN PQ.
c) Cm rằng nếu MP=PQ=QN thì a=2b
Cho tứ giác ABCD
Chứng minh:
a) Tổng 2 cạnh đối nhỏ hơn tổng 2 đường chéo
b) Nếu AD + AC bé hơn BD +BC thì AD bé hơn BD
1) Cho tứ giác lồi ABCD có góc B + D= 180°, CB= CD. Chứng minh AC là tia phân giác góc BAD
2) Tứ giác ABCD có AC là tia phân giác góc A, BC= CD, AB<AD
a) Lấy điểm E trên cạnh AD sao cho AE= AB. Chứng minh rằng góc ABC= AEC
b) Chứng minh góc B+ D= 180°