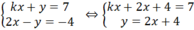
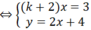
Với k + 2 ≠ 0 ⇔ k ≠ -2 thì hệ phương trình có nghiệm :

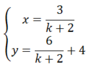
Ta có:

P = x 2 + y 2 = x 2 + 2 x + 4 2

= 5 x 2 + 16 x + 16  

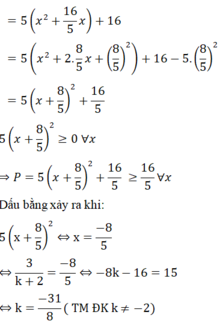
Vậy với k = (-31)/8 thì biểu thức P = x 2 + y 2  đạt giá trị nhỏ nhất

a) Ta có hệ phương trình \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\) Thay nghiệm \(\left(x,y\right)=\left(2,-1\right)\) ta có hệ mới là :

\(\hept{\begin{cases}2k-1=5\\2-1=1\end{cases}\Leftrightarrow k=3}\)

b) Ta có : \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}y=1-x\\kx-1-x=5\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}y=1-x\\x\left(k-1\right)=6\end{cases}}\)

Để hệ phương trình có nghiệm duy nhất : \(\Leftrightarrow k-1\ne0\) \(\Leftrightarrow k\ne1\)

Để hệ phương trình vô nghiệm \(\Leftrightarrow k-1=0\Leftrightarrow k=1\)

P/s : Em chưa học lớp 9 nên không biết cách trình bày cho lắm :))

Chọn đáp án C.

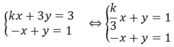
Do đó 2 hệ phương trình 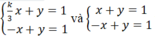tương đương khi k/3=1 ⇔k=3

 hệ pt trên tương đương:\(\hept{\begin{cases}x=3-ky\\k\times\left(3-ky\right)+4y=6\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}x=3-ky\\-y\left(k^2-4\right)=6-3k\end{cases}}\)

*với k=2 ,hệ pt có vô số nghiệm.*với x=-2,hệ pt vô nghiệm.* với \(x\ne\pm2,\)hệ pt tương đương:

\(\hept{\begin{cases}x=3-ky\\y=\frac{6-3k}{-\left(k^2-4\right)}\end{cases}\Leftrightarrow\hept{\begin{cases}x=3-ky\\y=\frac{3}{k+2}\end{cases}}}\)\(\Leftrightarrow\hept{\begin{cases}x=3-\frac{3k}{k+2}\\y=\frac{3}{k+2}\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{6}{k+2}\\y=\frac{3}{k+2}\end{cases}}\)

vậy \(\hept{\begin{cases}x>1\\y>0\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{6}{k+2}>1\\\frac{3}{k+2}>0\end{cases}\Leftrightarrow\hept{\begin{cases}k+2< 6\\k+2>0\end{cases}}}\)\(\Leftrightarrow-2< k< 4\)

VẬY HỆ PHƯƠNG TRÌNH ĐÃ CHO CÓ NGHIỆM X>1,Y>O KHI VÀ CHỈ KHI -2<K<4 VÀ K\(\ne2\)

tick mk đi chứ bài khó lắm

lam sao moi ra dc the chu pn