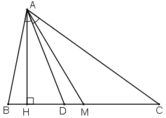
1, Cho tam giác ABC có ba đường trung tuyến AD; BE và CF. Từ F kẻ đường thẳng song song AD cắt ED tại I.
a) CMR: IC// BE
b) CMR: nếu AD vuông góc với BE thì tam giác ICF vuông.
c) So sánh các cạnh của tam giác ICF với các đường trung tuyến của tam giác ABC.