Cho tam giác abc có AM, BN, CP là đường cao sao cho BC+AM=AC+BN=AB+CP Chứng minh tam giác ABC đều

Những câu hỏi liên quan
Cho tam giác abc có ba đường trung tuyến AM,BN,CP cắt nhau tại G. Chứng minh rằng:
AM+BN+CP<AB+AC+BC
Cho tam giác ABC đều. Gọi M,N,P lần lượt trên AB,BC,AC sao cho tam giác MNP đều. Chứng minh rằng AM=BN=CP
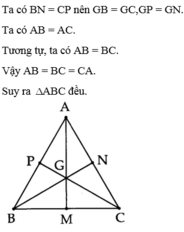
Cho tam giác ABC có ba đường trung tuyến AM, BN, CP cắt nhau tại G.
Biết AM = BN = CP. Chứng mình tam giác ABC đều.
Cho tam giác ABC đều trên cạnh AB, BC,CA lần lượt lấy điểm M,N,P sao cho AM=BN=CP. Chứng minh tam giác MNP là tam giác đều
Cho Tam giác ABC với ba đường trung tuyến AM , BN , CP và trọng tâm G .Chứng minh rằng
a, AM < ( AB + AC )
b, ( AB + AC + CA ) < AM + BN + CP < AB + BC + CA
Bài 5. Cho tam giác ABC có ba đường trung tuyến AM, BN, CP. Chứng minh rằng AM, BN, CP là độ dài ba cạnh của một tam giác.
Bài 5. Cho tam giác ABC có ba đường trung tuyến AM, BN, CP. Chứng minh rằng AM, BN, CP là độ dài ba cạnh của một tam giác.
cho tam giác ABC có trọng tâm G #đường trung tuyến AM : BN ; CP
CM 3(AM+BN+CP)<2(AB+BC+AC
Cho tam giác ABC , đường trung tuyến AM , BN , CP . Chứng minh BN +CP > 3/2 BC
Gọi G là trọng tâm tam giác ABC
Vì là trung tuyến \(\Rightarrow\hept{\begin{cases}BN=\frac{3}{2}BG\\CP=\frac{3}{2}CG\end{cases}}\)
\(\Rightarrow BN+CP=\frac{3}{2}\left(BG+CG\right)\)
Mà theo bđt trong tam giác cho tam giác BGC thì \(BG+GC>BC\)
\(\Rightarrow BN+CP>\frac{3}{2}BC\)
Đúng 0
Bình luận (0)