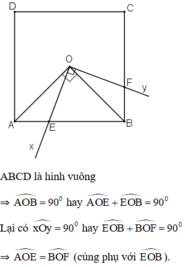
Cho hình vuông ABCD có AB = 16cm, AC cắt BD tại O. Một góc vuông xOy, có tia Ox cắt cạnh AB tại E, tia Oy cắt cạnh BC tại F. Tính diện tích tứ giác OBEF?

Những câu hỏi liên quan
Cho hình vuông ABCD có tâm đối xứng O , cạnh a . Một góc vuông xOy có tia Ox cắt cạnh AB tại E, tia Oy cắt cạnh BC tại F . Tính diện tích tứ giác OBEF?
Cho hình vuông ABCD có AB = 16cm, AC cắt BD tại O. Một góc vuông xOy, có tia Ox cắt cạnh AB tại E và tia Oy cắt cạnh BC tại F. Khi đó diện tích tứ giác OEBF là …cm2.
từ O hạ đường cao OH,OK ứng với AB và BC => OH=OK=8cm
có tgAOE=tgBOF (g.c.g) do
góc AOE=góc BOF (cùng phụ với xOy)
OA=OB
góc BOA= góc ABO (cùng phụ với góc ABO)
=> AE=BF
SOEBF = SEOB + SBOF = OH.EB/2 + OK.BF/2= OH( EB/2 + BF/2)= OH.((EB+AE)/2 )=(8.16)/2=64 cm2
SOEBF= SEOB + SBOF =
Đúng 0
Bình luận (0)
Cảm ơn bạn Nguyễn Đức Huy nhiều nhé.
Năm mới chúc bạn luôn mạnh khỏe, hạnh phúc và làm việc gì cũng thành công nhé.
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh 15cm tâm O. Một góc vuông xOy sao cho tia Ox cắt AB tại E, tia Oy cắt BC tại F. Tính diện tích tứ giác OEBF
Cho hình vuông ABCD có tâm đối xứng O, cạnh a. Một góc vuôn xOy có tia Ox cắt cạnh AB tại E, tia Oy cắt cạnh BC tại F (h.161). Tính diện tích tứ giác OEBF.
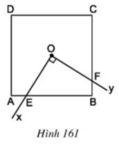
Cho hình vuông ABCD có tâm đối xứng là O, cạnh = a. Một góc vuông xOy có tia Ox cắt AB tại E, tia Oy cắt BC tại F. Tính diện tích tứ giác OEBF
ABCD là hình vuông
\(\Rightarrow\widehat{AOB}=90^o\)hay \(\widehat{AOE}+\widehat{EOB}=90^o\)
Ta lại có : \(\widehat{xOy}=90^o\)hay \(\widehat{EOB}+\widehat{BOF}=90^o\)
\(\Rightarrow\widehat{AOE}=\widehat{BOF}\)( cùng phụ với \(\widehat{EOB}\))
+) Xét 2 tam giác : AOE và BOF , có :
OA = OB
\(\widehat{OAE}=\widehat{OBF}\left(=90^o\right)\)
\(\widehat{AOE}=\widehat{BOF}\left(cmt\right)\)
\(\Rightarrow\Delta AOE=\Delta BOF\left(g-c-g\right)\)
\(\Rightarrow S_{AOE}=S_{BOF}\)
\(\Rightarrow S_{AOE}+S_{OEB}=S_{BOF}+S_{OEB}\)
hay \(S_{AOB}=S_{OEBF}\)
Mà \(S_{AOB}=\frac{1}{2}S_{ABCD}=\frac{a^2}{4}\)
\(\Rightarrow S_{OEBF}=\frac{a^2}{4}\)
Cho hình vuông BCD có tâm đối xứng O, cạnh a. Một góc vuông xOY có tia Ox cắt cạnh AB tại E, tia Oy cắt cạnh BC tại F (h.161)
Tính diện tích tứ giác OEBF ?
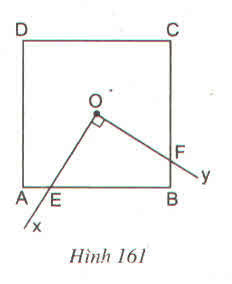
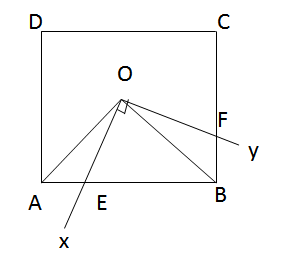
Nối OA, OB.
Xét \(\Delta\)AOE và \(\Delta\)BOF có:
+ \(\widehat{AOE}=\widehat{BOF}\) (cùng phụ với \(\widehat{BOE}\))
+ OA = OB (O là tâm đối xứng)
+ \(\widehat{OAE}=\widehat{OBE}=45^o\)
=> ∆AOE = ∆BOF (g - c - g)
Do đó: \(S_{OEBF}=S_{OEB}+S_{OBF}=S_{OEB}+S_{OAE}=S_{OAE}+S_{OEB}=S_{OAB}\)
Vậy \(S_{OEBF}=\dfrac{1}{4}S_{ABCD}\)
Đúng 0
Bình luận (0)
Nối OA, OB.
Xét ΔAOE và ΔBOF có:
+) \(\widehat{AOE}=\widehat{BOF}\) ( cùng phụ với BOE )
+) OA = OB ( O là tâm đối xứng )
+) \(\widehat{OAE}=\widehat{OBF}=45^0\)
⇒ ΔAOE = ΔBOF.
⇒ \(S_{OEBF}=S_{OEB}+S_{OBF}=S_{OEB}+S_{OAE}=S_{OAE}+S_{OAB}\)
⇒ \(S_{OEBF}=\frac{1}{4}S_{ABCD}.\)
Cho hình vuông ABCD có cạnh bằng a cm. Gọi O là giao điểm 2 đường chéo. Góc vuông xOy, tia Oc cắt BC tại E, tia Oy cắt CD tại F. Tính diện tích tứ giác OECF
Cho hình vuông ABCD có AB = 16cm, AB cắt BD tại O. Một góc vuông xOy, có tia Ox cắt cạnh AB tại E và tia Oy cắt cạnh BC tại F. Khi đó diện tích tứ giác OEBF là ...cm2
Cho hình chữ nhật ABCD có AB12cm, AD6,8cm. Gọi H,I,E,K là các trung điểm tương ứng của BC,HC,DC,EC. a) Tính diện tích tam giác DBE . b) Tính diện tích tứ giác EHIK.Cho hình vuông ABCD có tâm đối xứng O, cạnh a. Một góc vuông xOy có tia Ox cắt cạnh AB tại E, tia Oy cắt cạnh BC tại F. Tính diện tích tứ giác OEBF.
Đọc tiếp
Cho hình chữ nhật ABCD có AB=12cm, AD=6,8cm. Gọi H,I,E,K là các trung điểm tương ứng của BC,HC,DC,EC. a) Tính diện tích tam giác DBE . b) Tính diện tích tứ giác EHIK.Cho hình vuông ABCD có tâm đối xứng O, cạnh a. Một góc vuông xOy có tia Ox cắt cạnh AB tại E, tia Oy cắt cạnh BC tại F. Tính diện tích tứ giác OEBF.
Bài 2 :
Các tia đối Ox,Oy cắt CD, DAtheo thứ tự G, H
Do t/c đối xứng nên diện tích tứ giác OEBF = dt tứ giác OFCG = dt tứ giác OGDH= dt tứ giác OHAE
Mà tổng diện tích 4 tứ giác đó = dt hình vuông ABCD = a2
=> Diện tích tứ giác OEBF = \(\frac{a^2}{4}\)